Exploring Proportionality through Measurement and Geometry
Bruce Olberding (NMSU Math) and Maribeth Olberding (NMSU Math-Ed)
with the assistance of
Sharon Brooks (Math Teacher, West Monroe High) and Stephanie Welch (ULM Math-Ed undergraduate)
January 22, 2004
Introduction
One of the main goals of our project was to design an application of readily accessible mathematics to a physical problem in a non-trivial way. Often the first applications of mathematics to physical situations that students (both secondary and undergraduate) see are not particularly powerful examples. We attempted to design a project that would provide a convincing and historically important application of elementary mathematics by basing our project on a 3rd century C.E. Chinese surveying text, The Sea Island Mathematics Manual.[1] In this project students are required to perform measurements of inaccessible objects (for example, large buildings) by the use of sighting poles and the Theorem of Similar Triangles. While it is not unusual for high school students to see applications of this theorem to measurement, the surveying methods of Sea Island require the use of two pairs of similar triangles, solving a system of equations and some geometrical insight. By a more intensive use of the Theorem of Similar Triangles, the students are able to make measurements of distant objects without approaching them. Class discussions emphasize the historical importance of this skill to help the students further their understanding of the mathematical concepts.
I. Mathematical Discussion
A. Applicability of mathematics to physical problems
It is not unusual for high school students to have seen the theorem of similar triangles used to measure the height of, say, a telephone pole or tree.[2] This is an interesting example and it is well-suited to the secondary level, but it involves what are often unrealistic assumptions—in particular, one typically measures the distance from the telephone pole (or tree) to the observer or sighting pole, and this distance can be quite large. This works sufficiently well with some objects, like a telephone pole, but it requires that the object be quite narrow. By contrast, this method poses difficulties in the measurement of, for example, one of the Great Pyramids. (The base of the pyramid must be accounted for in the measurement.) Also, there are numerous applications where one can only perform “local” measurements in the near vicinity of the observer; in this case, one may not be able realistically to measure the distance between observer and the object of measurement.
Thus this typical application of similar triangles has a number of shortcomings as an actual technique of measurement. From a pedagogical point view, it also does not make a very deep use of the theorem of similar triangles. In order to intensify the mathematics in the use of similar triangles for measurement, and to help demonstrate its powerful applicability, we have centered our project on a 3rd century C.E. Chinese surveying text: The Sea Island Mathematics Manual. This particular text outlines methods for measuring a number of inaccessible objects (sea bluffs, deep ravines, lengths of fortress walls, etc.). The main method requires the use of two sighting poles, rather than the one that is often seen in textbook examples of the use of similar triangles. The use of two sighting poles has the advantage of allowing the observer to perform only local measurements. The trade-off for this added power is that now the observer must deal with two sets of pairs of similar triangles. Ultimately this produces a system of two linear equations in two unknowns that must be solved. Hence the algebraic manipulation required to solve the problem is more substantial than the traditional textbook version of the measurement problem, which requires the solution of a single linear equation in one unknown.
B. Proportionality and similar triangles
The basic tool in our use of measurement is the theorem of similar triangles. Students gain familiarity with this concept by employing it to solve problems involving measurement; then later in the activity, they explore how it can be used to provide a foundation for the notion of the tangent function. Also, on the last day of the activity, they explore an interesting proof of this theorem using the “out-in complementary principle” of Liu Hui’s surveying text.
C. Systems of linear equations
The Sea Island method of measuring inaccessible distances involves the analysis of two pairs of similar right triangles. This yields a system of two linear equations in two unknowns which must be solved in order to obtain the desired measurements. Thus the activity reinforces the importance of systems of linear equations in applications.
D. Modeling
After attempting some of the difficult measurements (e.g. measuring the height of a distant tower), the students better appreciates some of the obstacles to modeling a physical situation using mathematics. We designed our project so that the students would first attempt the measurement of a campus tower without knowledge of the Sea Island method. This poses a number of obstacles to modeling, and the first stage of the activity is meant to encourage students to document these difficulties. Once they see the obstacles involved, they better appreciate how mathematics can be used to help surmount some of the difficulties.
E. Geometrical origin of the tangent function and an example of an invariant
On the last day of the activity the students explore how, corresponding to a fixed angle θ, one may associate a ratio (the tangent) that depends only on the given angle θ. That this ratio depends only on the angle θ is justified using similar triangles. It is also illustrates that the ratio is an invariant of an equivalence class (under similarity) of a given right triangle.
II. Pedagogical Discussion
A. Applicability of mathematics
It is extremely important for future teachers to be convinced of—and to have experience with—the applicability of mathematics. A familiarity with and appreciation for this applicability can be communicated to secondary students, who too often encounter the problem of wanting interesting applications of mathematics yet not having the mathematical or scientific sophistication necessary to understand such applications. With this in mind we have tried to design our activity so that most if not all of it can be transferred to a high school Geometry or Algebra II class.
At the same time, we have sought to make the project interesting to mathematically sophisticated undergraduates. While the activity really requires no mathematics beyond the high school level, it does demand a mature approach to problem-solving. It also synthesizes several aspects of geometry (similar triangles), linear algebra (systems of linear equations) and trigonometry (the tangent function as a function) in a way that is not typically seen in a single course in the undergraduate curriculum. We believe that this synthesis of different subject areas in mathematics is very important in the preparation of future secondary teachers.
We have also purposely designed a major part of the activity to take place “off the paper.” By having the students attempt difficult measurements outdoors, the activity helps to give future teachers a robust sense of what mathematics entails. Throughout the activity, the students appeared more comfortable with the abstraction of mathematics rather than its application. This is to be expected since most of one’s mathematical training involves such abstraction, but it is useful to keep in mind how much of mathematics was developed to model physical situations.
B. Historical motivation
In order to emphasize the historical importance of indirect measurement, our team chose to make the centerpiece of the activity the 3rd century Chinese surveying text, Liu Hui’s The Sea Island Mathematics Manual. By discussing this text and its cultural importance with the students, the mathematics behind it is humanized to an extent that is sometimes unusual in an undergraduate class. One of the main goals of the activity is to provide a compelling application of mathematics, and we feel that discussing this application in a historical context helps make this a particularly nice application of relatively simple mathematics.
C. NCTM Standards
The publication of the National Council of Teachers of Mathematics (NCTM) Standards documents (1989, 1991, 1995, 1998, 2000), focused significant attention on curricula, professional development, and assessment issues as they relate to the teaching and learning of mathematics. The message contained in these documents had a significant impact on the development and implementation of the plan for this proposed project. As is noted in the Principles and Standards (2000), the world today is dramatically different from what it was in 1989 when the first Standards document was published. Student access to computers and the World Wide Web is now common, whereas in 1989 the availability of handheld scientific and graphing calculators was uncommon. Anything that has been algorithmized can be done by a computer. This means that actually performing a calculation is no longer a problem about which most people have to worry. Rather, what requires attention is determining what calculation to do. In short, people now need more understanding and less procedural skill. The practice of collecting and representing data from real world settings and then applying a mathematical concept to that skill is another leap in the direction that modern mathematics has taken us. Our project focuses on the application of these skills by learning from historical sources how to apply the knowledge of their modern day world to that used in the 3rd century from Sea Island Mathematics Manual.
III. Lesson reports and student work
This activity was conducted by Maribeth Olberding (team educator) in her junior-level Modern Geometry course in Spring 2002. The class consisted of 10 students, 5 of whom were mathematics education majors. Students were divided into three groups. They maintained these same groups throughout the activity. A MWF class, the activity took place over three class meetings during the span of one week. Prior to this activity, the students spent the first week of class by studying Oliver Byrne’s colorful version of Euclid’s Elements[3] as a quick (and rather novel) review of the nature of geometrical arguments.
Day 1. The activity began with a warm-up problem meant to reinforce the notion that physical situations often require indirect measurement. This warm-up problem took approximately 35 minutes. Despite the amount of time devoted to this rather simple exercise, we believe it worthwhile to get the students thinking about the difficulties sometimes involved in indirect measurement.
Warm-up activity: Using a yardstick, find the perimeter of the following objects: Group A, classroom door; Group B, one panel of the classroom blackboard; Group C, classroom window.
The students, as members of a junior level mathematics course, were suspicious of this exercise. Although they approached it with good humor, they appeared to be surprised by having to accept the imprecision in the use of yardsticks. One surprising outcome of this experiment is it revealed how, despite the training and sophistication of the class members, a very simple application of mathematical ideas to physical problems could raise naïve questions. It provided an interesting contrast to the confidence with which the students had approached the abstract setting of Euclid’s Elements the previous week.
Group A began the exercise with a long discussion of how the problem was “too easy.” Group C began with a curious discussion of whether it mattered if the measurement was made from the top to the bottom of the window, or vice versa. All groups, despite their initial discussions, quickly completed their assignments.
In-class problem: Find the length of the diagonal of the door (blackboard, window).
A student in Group A began
this exercise by attempting to measure the diagonal using the yardstick. She
was stopped by the members of her group, who asked the instructor, “Do we do
this by hand?” The instructor simply shrugged and left the students to decide
for themselves whether to use a yardstick or not. Group C, wanting to use
trigonometry, debated whether or not this would be appropriate if the diagonal
was at 45 degrees. (They apparently wanted to be certain that the angles
involved corresponded to memorized values for the trigonometric functions!)
Finally all groups settled on the Pythagorean theorem as not only easier, but
more accurate, since the diagonal was hard to follow with a yardstick.
 |
Follow-up Problem (all groups): Measure the length of the diagonal of the classroom.
In this problem, there was no debate. The students, taking into account the size of the room and the clusters of desks blocking potential measurements, immediately agreed that it was easiest and more accurate to measure the diagonal via the Pythagorean theorem. The tile floor of the classroom allowed them a further simplification: they measured one tile, then counted tiles to arrive at a quick estimate of the measure of the diagonal.
Discussion (approximately 10 minutes): The students were asked to return to their seats, and the instructor related the traditional legend of Thales measurement of the pyramids by shadow reckoning. She drew a pyramid on the chalkboard with Thales a good distance away. She asked the students to indicate possible problems for Thales in seeking to measure the height of the pyramid. The students quickly pinpointed a number of problems such as the awkward shape of the pyramid (how does one measure it’s altitude?), and the difficulty of devising a long enough yardstick or tape measure. The instructor then asked for suggestions on how Thales could measure the pyramid. One participant in the class, a teacher seeking mathematics certification, suggested similar triangles. The students reminded each other of the theorem of similar triangles that, in their words, “corresponding sides are proportional.” This also led to a discussion among the students of the difference between similar and congruent triangles.
The instructor related a version of the legend of how Thales used the sun and shadows to measure the height of the pyramid. Thales paces a straight line away from the pyramid until he can sight the sun just over the tip of the pyramid. Having measured the distance from the pyramid, he measures now the length of his shadow. He knows also his height, so using a pair of similar triangles, he calculates the height of the pyramid.
To close the class, the instructor assigned the following group project to be completed by the next class period. The students maintained their same in-class groups for this project.
Group Project 1 (Due next class period):
Measure the height of the tower of the Administration Building
on the ULM campus. Discuss the reliability of your measurements
and any obstacles you encounter in making your measurement.
The students asked questions about how they were supposed to accomplish this. The instructor deliberately gave no clues.
Day 2. The students began the next class period by discussing the successes and failures of their attempt to measure the Administration Building tower. The instructor asked whether the groups had been successful in their measurements. The students, despite a diversity of methods (discussed below) used to solve the problem, expressed confidence in their measurements. They were reassured by the fact that all 3 groups found the height to be with the range of 95 to 115 feet. When pushed further on this point, however, they agreed that this was probably too significant of an error to make their measurements useful.
Group B. This group tried three different methods to measure the height of the tower.
(1) We just looked at it and estimated the height by our personal imagination. We figured it to be about 120 feet. This is obviously not very reliable or accurate, but it gets you started. To estimate it just by looking at it would be more accurate if you knew the height of a building close to it and could compare them.
(2) Next we counted the windows on the tower and multiplied that (18) by the length of one window (68 inches) which is about 102 feet. This is much more accurate, except the top window is perhaps longer or shorter than the others, but we are probably within 2 feet.
(3) Next we used the legend of Thales to get the height of a light pole in front of the tower. We lined up the end of one of our shadows with the end of the pole’s shadow. We then measured the length of our shadow as well the shadow of the pole. After we knew the height of the pole (19.8 feet), we measured the distance from the pole to the tower (84 feet). We then put our face on the ground in a straight line with the pole and edge of the tower. We moved back until our head lined the top of the pole with the top of the tower. [This discussion was accompanied with a diagram and a calculation that finds the height of the tower to be 106.2 feet.] This is a fairly accurate approach, except since shadows are not definite lines, you are dealing with estimates. You must wait until the shadows are longer to reduce the roundings [?] and make for more exact figures.
Method (3) is interesting in that the students sought to use shadow-reckoning but found that, while simple to understand, it was difficult to achieve in practice. Note that the students did not actually use their shadow measurements; evidently they felt compelled to carry them out in order to mimic what Thales did, even though the information proved extraneous for them.
Group A. This group tried 3 different ways. They stated, “We did not use the legend of Thales or trigonometry because the shadow was going across the top of [another] building and could not be measured.” Note that this group did not recognize that Thales method could also be applied without shadows.
(1) The students first tried the same method as (2) of Group B. Measuring a window and multiplying by the number of windows, they arrived at a height of 102 feet and 2 inches. They recognized that “The error in this method is having to estimate the height of the stucco panel at the top….We are also assuming that all the panels are exactly the same. If this is not true then our error will be greater.”
(2) For their second method, the students turned to the Internet. There they discovered (on a website entitled “Bizarre Stuff”!) how to use a device called a “hypsometer” to measure the height of a tree. The website discussed how to use a yardstick as a hypsometer. “Stand exactly 25 feet from the tree being measured. Hold the yardstick, with the zero end downward, 25 inches from your feet. Line up the bottom of the yardstick with the base of the tree. Without moving your head, look to the top of the tree. Where it crosses the yardstick, read of the measurement in inches. Each inch will equal one foot in the tree’s height.”[4] The students used the hypsometer to measure the tower as 114 feet high. They stated that “the error in this method is the accuracy of our measurement, both the 25 feet segment and the 25 inches from our eye to the yardstick. Looking up without moving your head also leaves room for error.”
(3) The third approach of Group A was particularly
novel. “We attached ribbon to a bunch of helium balloons. [See picture.] The
balloons were then raised to the top of the tower, and we measured the ribbon.
This was the least accurate of our methods because of the wind. We did this
twice and the wind was blowing in the opposite direction, so we decided to
average our 2 tries.” They computed the height with this method to be 106
feet. “The more times you do this, the closer your answer will be.”
Group C. This group tried two methods. In the first method, which was also but the other two groups, they measured the height of a window on the tower and multiplying according to the number of windows. They arrived at a height of 103.92 feet. In the second, they used similar triangles in a fashion similar to that of Group B, method (3). They calculated the height of the tower to be 114.9 feet.
Conclusion: We view this group project as a good way to emphasize the difficulty of putting mathematical ideas into practice. In fact, the students appeared the most confident in their estimates that used a minimum of mathematical reasoning, namely measuring the height of a window and multiplying by the number of windows. Despite the juxtaposition of the story of Thales with the assignment of the group problem, the students appeared distrustful of their estimates achieved using this method.
We were pleased with the novelty of some of the students’ solutions, such as the use of the hypsometer or the balloons. Also, we had not anticipated that the students would use the windows as a means to measure the tower. We were pleased in the students desire to try several methods in order to confirm their estimates. As mathematics educators, we would have liked to have seen the students introduce novel mathematically based approaches to this project. Yet viewed against the background of history, the introduction of new mathematically based approaches to measurement is a rather exceptional occurrence.[5]
Sea-Island Discussion: After discussing the successes and failures of the measurement of the height of the tower, the students were presented with a new twist on this same problem: Would it be possible to measure the tower if one were not allowed to approach it? The students agreed that the methods they used would not work in this case. The instructor posed the question of whether the remote measurement of a distant object could be useful. The students immediately offered situations (a very distant object, an object across a canyon, etc.) in which such measurements would be useful. The discussion led to military applications of indirect measurements (e.g. the height of a castle wall); this appeared to be one of the most convincing applications of indirect measurements.
At this point the instructor introduced The Sea Island Mathematics Manual, and pointed out that as early as 263 C.E. the Chinese were employing sophisticated arguments involving sets of similar triangles to measure inaccessible distances.[6] The motivating example is that of Sea Island, a distant bluff separated from the observer by a small sea. Liu Hui, the author of the text, outlines a solution for this problem that involves only “local” measurements, that is, measurements that can be accomplished in the near vicinity of the observer. The basic idea is to plant two same height sighting poles, or “gnomons,” a fixed and measurable distance apart (see figure below.)
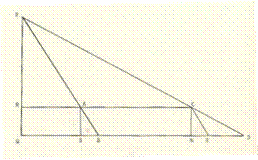The poles lie on a line emanating from Sea Island.
Lying on the ground, the observer then sights the top of Sea Island over the
top of each pole; the distances A and B from each sighting position to the
sighting pole are then measured. The following five measurements are known:
the height of the poles, the distance between the poles, and the two distances
A and B. Note that all five of the distances are easily obtained in the
immediate vicinity of the observer. Using the theorem of similar triangles, it
is now possible to compute the height h of Sea Island; also, this same
computation produces (rather than requires!) the distance d from the first
sighting pole to Sea Island.
To reinforce the Sea Island method, the students were given the following in-class activity to simulate the use of sighting poles.
In-Class Group Project (approximately 30 minutes): Using yardsticks as sighting poles, measure the following distances using the Sea Island method: Group A: floor to the top of the chalkboard; Group B: height of classroom door; Group C: floor to the top of window.
Since these measurements had to be accomplished in a very small space, the students were given fishing line to simulate the line of sight. This also allowed the students to visualize the formation of the sets of similar triangles to be used in the computation of the heights.[7]
In completing the in-class assignment, all three groups encountered difficulties in obtaining their measurements. For example, one group pointed out that the measurements would be incorrect if the fishing line was not taut. Another group discussed whether or not the problem could be solved if the “shadows” of the sighting poles (i.e. the base of the small right triangle formed by the sighting pole and the fishing line) overlapped. Reaching no conclusion, they simply moved their sighting poles farther apart until the “shadows” no longer overlapped.
 |
|||
 |
|||
To end this class period the three groups were given a new project:
Group Project 2: (Due next class period) (a) Use the Sea Island method to measure the height of the tower on the administration building. (This is the tower that they were asked to measure last time.) (b) Measure the height of the campus bridge over Bayou Desiard. (The students were not told to use the Sea Island method for this measurement. We wanted to see if they would adapt the method to this rather different setting.)
The students were also given a bonus challenge problem:
Challenge Problem: (Due next class period) Measure the height of the administration building from the seventh floor of the university library. All measurements must be obtained while positioned on the seventh floor of the library.
Day 3. The three groups returned the next class
period with completed projects. Groups A and B found the height of the tower
to be approximately 100 and 102 feet, respectively. Group C found the height
to be about 123 feet. All three groups used the Sea Island method correctly.
Group B commented that the “obstacles are keeping meter sticks perpendicular
and the grass isn’t completely flat.” In class the students also commented
that it also could be difficult sighting the top of the building while lying on
the ground.
All 3 groups were able to successfully adapt the Sea Island method to the measurement of the height of the bridge above Bayou Desiard. Group A found the height to be 15 feet 3 inches. Group B measured the height at 186.35 inches. Group C measured the height at 13.46 feet. Group A confirmed their measurement by lowering a stick on a string from the top of the bridge till it touched the water. They then measured the length of the string at 15 feet 1 inch. They stated, “We did this method because we wanted to be more sure of our measurement from Liu Hui’s [Sea Island] method.”
Only one group (Group C) attempted the challenge problem. The challenge problem can be solved by a modification of the Sea Island method. However, the yardsticks have to be used in a different way. Liu Hui solves this problem in The Sea Island Mathematics Manual by the use of carpenter squares, which can be formed by joining the ends of the two yardsticks to form a right angle. Ultimately the problem reduces to two sets of similar triangles (cf. page 49 of Sea Island).
Group C was not able to adapt the Sea Island method to this measurement of the height of the administration tower from the 7th floor balcony of the library. However, they did use an imaginative method to obtain the measurement.
We measured the distance from the bottom of the 6th floor to the bottom of the 7th floor (= 191.5 inches). This allowed us to determine the height from the ground to the top of the 6th floor (= 1149 inches).[1] While standing on the 7th floor balcony, we realized that we were not quite as high as the tower. This presented us with a problem. How do we estimate the height remaining [i.e. the difference in height between the library’s 7th floor balcony and the administration tower]? The solution was not in front of us, but behind us. We found the reflective windows of the library [which were behind them] and were able to use the image before us as a gauge. Using the treeline as a reference point, we took notice of where our eyes were lining up with the tower. We used Sam’s eyes because his fell right at the top of the highest pane of stained glass [on the administration tower]. His eyes are 65.25 inches off the ground. With only the height of the concrete section of the very top of the tower unknown, we estimated it to be half of a window pane [on the tower] by observation from the balcony. We measured the height of a window pane and then put the numbers together (= 103.95 feet to the top of the administration tower).
The students located three sources of possible error: “(1) The height of each floor of the library should be consistent, however it may be a little off; (2) Even though the reflection in the mirror [reflective glass] appeared to be a true representation, it could have shown a slight distortion; (3) Estimating the top concrete section to be half of [administration tower’s] stained glass window pane.”
In the class discussion that followed, the students expressed confidence in their measurements of the Administration tower. However, they all recognized that small errors in their measurements using the sighting poles could translate into large errors in the computation of the height of the tower.
At the close of the discussion, the students inevitably asked for the “right” answer, namely, what is the height of the administration tower? They were unhappy to learn that they were the experts on its height. While of course it would be possible to learn the height of the tower from data the university keeps on its buildings, we felt it better to leave this a mystery, since the point of the Sea Island Method is to measure inaccessible distances and to gain confidence in the mathematics that replaces direct measurement.
Follow-up assignment: In addition to the Sea Island problem, there are 11 other surveying problems in the Sea Island Mathematics Manual, some of which are quite challenging. The instructor assigned two of these problems for homework:
Individual Homework Assignments: (a) Design a method using two sighting poles to measure the height of a pine tree on a hill; (b) Design a method using two sighting poles to measure the length of a fortress wall.[8]
This discussion and the assignment of the individual homework problems took approximately 10 minutes of the class period. The rest of the class period was devoted to further exploration of similar triangles. In particular, the instructor led the class through Liu Hui’s proof of the theorem of similar triangles using his “out-in complementary principle.” (See pp. 37-39 of Sea Island for a discussion of this proof.) This took approximately five minutes.
The class then explored an invariant for similar triangles, namely the ratio of the lengths of two sides. Of course, this ratio coincides with the tangent of an angle of the triangle, but the instructor did not mention this connection, preferring instead for the students to discover this on their own. This was accomplished through the following series of in-class group activities.
In-class activity: On a blank piece of paper positioned on its side, draw a horizontal line near the bottom of the page. (Inch grid paper also works very well for this exercise; in what follows, substitute “inch” for “centimeter.”) Draw a slanted line that meets the left endpoint of the horizontal line at an acute angle θ. Using a ruler, number marks every centimeter along the horizontal line. (See figure.) Draw a vertical line from each of the centimeter marks to form a series of trapezoids along the horizontal line.
 |
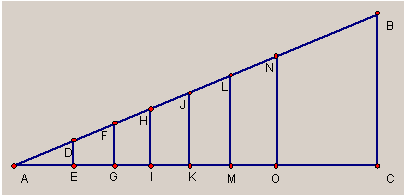View the diagram as compromised of a series of similar right triangles. Note that each triangle shares the angle θ (angle BAC in the diagram). Construct a table of measurements A and B, where A represents the length of the base of a triangle, and B represents the length of the side opposite the angle θ. Finally, in a third column, compute the ratio B/A. What do you notice? Can you explain what you observe?
After the students completed this activity, the instructor gathered the data from the students and asked them to explain how each group arrived at a different constant ratio. The students recognized immediately that the ratio should depend on the angle θ in the diagram. As each group had begun with a different diagram, the constant ratios differed also. The instructor summarized the conclusion: To each angle θ, one may associate a unique number. It can be computed as the ratio of the lengths of two particular sides of a right triangle with angle θ. In this way, one can define a function f(θ) = B/A, where B/A is computed as above (and of course depends on the angle θ ). At this point the instructor posed the question of whether this defines a new function? After some discussion, the students concluded that this is the familiar tangent function.[9] The instructor summarized this by emphasizing that our familiar tangent function can be shown to be well-defined because of the theorem of similar triangles.
III. Conclusion
By having the students discover for themselves many of the difficulties involved in collecting data and modeling a physical situation, we believe they achieved a greater appreciation of the powerful tool that mathematics can be in measuring inaccessible distances. By exploring the theme of similar triangles in a number of ways, we hope the future teachers in the class will think in a richer way about a fundamental theorem of geometry. As the activity progressed, the students traded complicated measurements and simple use of the Theorem of Similar Triangles for less complicated measurements and deeper use of this theorem. At the same time, they saw that mathematical insight (in particular the use of two sighting poles, rather than one) led to a more powerful means in which to obtain measurements of distant objects. This gave students a sense that the measurements get easier and more accurate as the use of mathematics involved becomes more sophisticated. As instructors we were pleased with the enthusiasm which the students undertook their projects and with the interesting and inventive approaches they discovered to some challenging problems.