The Area of a Triangle

The formula for the area of a triangle is:

area = one-half (length of the base) times (length of the the altitude).

You have to use the same linear units (inches, say) to measure the base and the altitude. The area is then given in square units (square inches, if we used inches to measure the sides).

How do you give a reasoned account of the formula, that is, an account that demonstrates why it is the "right way" to find a triangle's area? We cannot begin reasoning without some prior knowledge. We need to base our reasoning on something. We begin, therefore, assuming that we all already know and understand that the area of a rectangle is found by multiplying its length and its width.

Consider how we might determine the area of triangle ABC in the figure below:

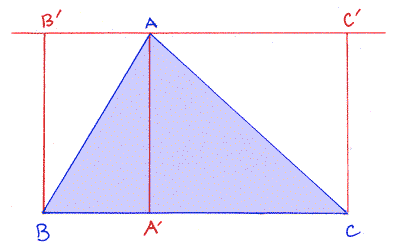
We've added a line through A that is parallel to the base BC, and we've marked points A', B' and C' to make 3 segments, each of which is perpendicular to BC.

Now the reasoned explanation can go as follows: Triangle ABC covers exactly one-half of the area in rectangle BCC'B'. But the area of this rectangle is |BC| | AA'| = (base of ABC)(altitude of ABC). The area of the triangle is half this.

Area ABC = (1/2) (base of ABC)(altitude of ABC)

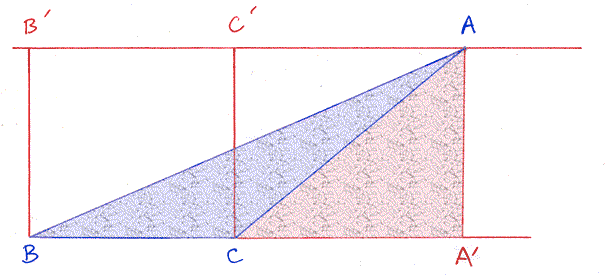
All seems well and good. However, this reasoning is not adequate for some triangles. What if A is not over the base? This situation is illustrated in the next picture:

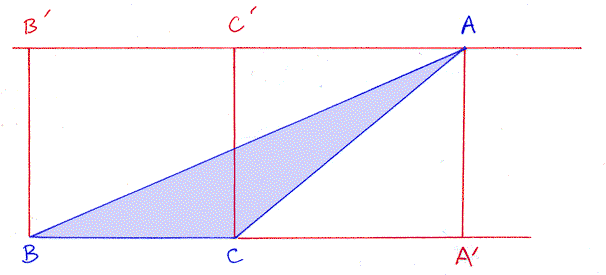
In this case, the reasoning has to be different.