Modes and transmission in periodic slabs

Through a series of diagrams, the concept of anomalous transmission induced by a nonrobust guided slab mode is explained. For simplicity, the scalar Helmholtz equation in two dimensions is used.

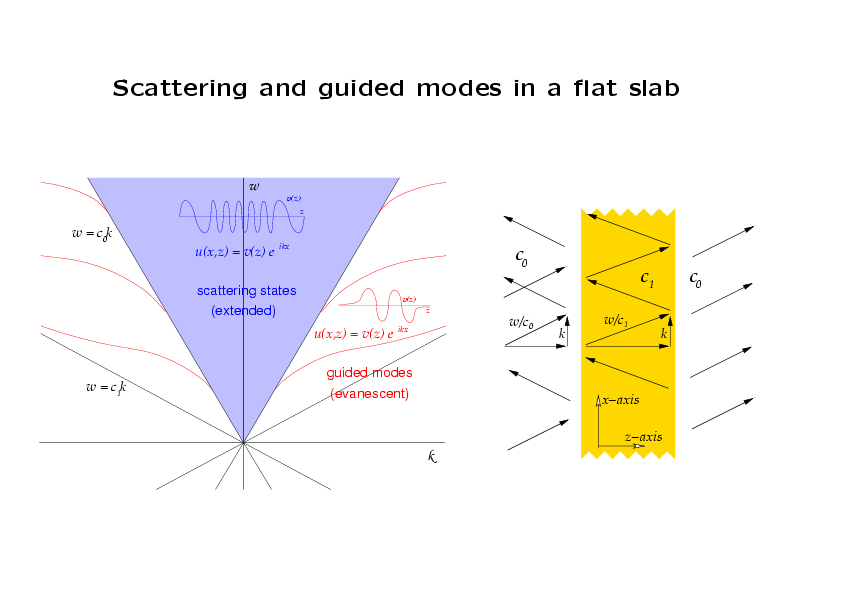
The diagram on the right depicts scattering of a plane wave by a uniform flat slab. The frequency is ω and the wave vector in the x-direction is k. The (free-space) speed of light in the air is c=c₀, and the (free-space) speed of light in the material of the slab is c=c₁. At frequency ω, the air supports waves of wave number ω/c₀, and therefore travelling waves in the air must have k≤ω/c₀, in other words, (k,ω) must be above the light cone ω=c₀k depicted in the (k,ω)-plane in the diagram to the left.

The field u satisfies the Helmholtz equation (∂_xx + ∂_yy)u + (ω/c)²u = 0. Since the structure is independent of x, we can consider solutions of the form u(x,z) = v(z)e^ikx. For each point (k,ω) above the light cone ω=c₀k, such solutions are constructed simply by matching oscillatory functions v(z) across the air-slab interface. The oscillations in the slab are tighter because c₁≤c₀ (as suggested by the graph of v(z) in blue). These are the "scattering states", or "extended states" of the air-slab structure.

The region between the cones ω=c₀k and ω=c₁k (the latter is the light cone for a space filled with the material composing the slab) is the (k,ω)-regime in which v(z) is exponential in the air and oscillatory in the slab. In order that the solution be bounded, it must decay as |z| tends to ∞. This only happens on certain "dispersion relations", calculated again by matching exponential functions in the air to oscillatory functions in the slab and demanding that the growing components vanish. These are indicated in red. Each point (k,ω) on any one of these relations corresponds to a "guided mode" of the slab, whose form is suggested by the graph of v(z) in red. They are "evanescent"--they decay into the air.

Pairs (k,ω) below the cone ω=c₁k do not admit Helmholtz fields.

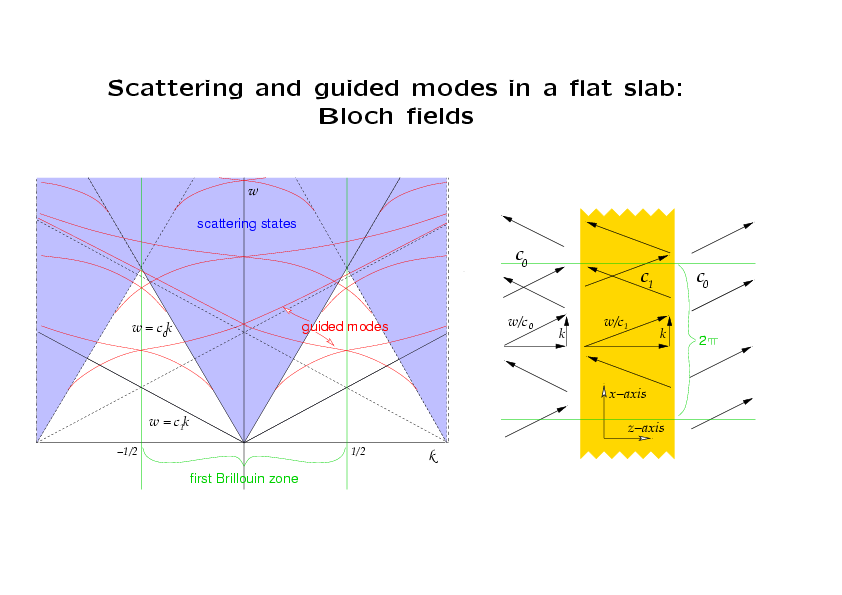
Let us now impose an artificial period of 2π in the x-direction and write each Helmholtz field u(x,z) = v(z)e^iKx as a function w(x,z) that is periodic in x, times e^ikx, where the "Bloch wave number" k lies in the first Brillouin zone [-1/2,1/2). Simply put K = k + n, where n is an integer, to obtain

u(x,z) = w(x,z)e^ikx

with

w(x,z)=v(z)e^inx.

Now, for each k in [-1/2,1/2), there corresponds a sequence of guided modes, whose frequencies are indicated by the red dispersion relations that have been "folded over" into this zone. Those that fall on the blue zone corresponding to scattering states can be thought of as frequencies of guided modes that are "embedded" in the continuous spectrum of extended states.

For a fixed value of k, the frequencies of these guided modes are eigenvalues embedded in the continuous spectrum of the Helmholtz operator restricted to pseudo-periodic fields in the infinite strip (0,2π)x(-∞,∞) with pseudo-periodic factor e^2πik. In the strip, the guided modes are square integrable.

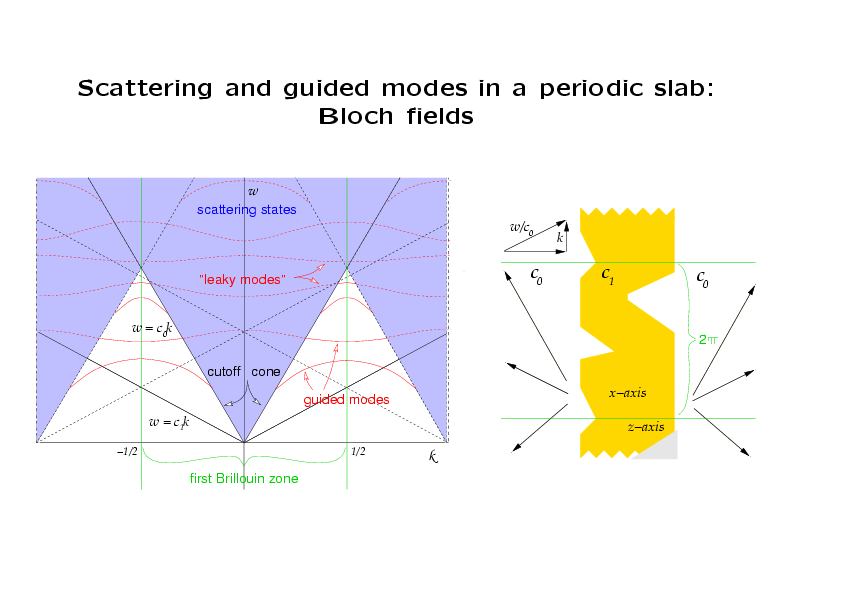
If we now impose a genuine periodicity upon the slab, the solutions are no longer separable, and the periodic factor w(x,z) in the Bloch fields attains all Fourier harmonics,

w(x,z) = Σ_n=-∞^∞ v_n(z)e^inx,

in other words, the Bloch wave number k is only determined up to an additive integer, so we take it to lie in the first Brillouin zone. To the left and right of the slab, the functions v_n(z) have the form

v_n(z) = a_n e^iη_nz + b_n e^-iη_nz,

(with different coefficients to the left and right) in which (ω/c)² - η_n² - (n+k)^k = 0 and η_n>0 if η_n²>0 and iη_n<0 if η_n²<0. We see that there are a finite number of propagating Fourier harmonics (η is real), and the rest are decaying, or evanescent, (η is imaginary). The Fourier harmonics are also called the Bragg harmonics.

Since the Bloch fields typically contain all Fourier harmonics, those with (k,ω) in the blue region above the cone ω=c₀k do not correspond to guided modes because at least one of the harmonics (n=0) is propagating. Thus the dispersion for guided modes disappears in that zone. Instead there is a complex dispersion relation D(k,ω)=0. The real part of ω is indicated by the dotted curves for real values of k. If the imaginary part of ω is very small, these curves correspond to "leaky modes" (we omit explanation of these here).

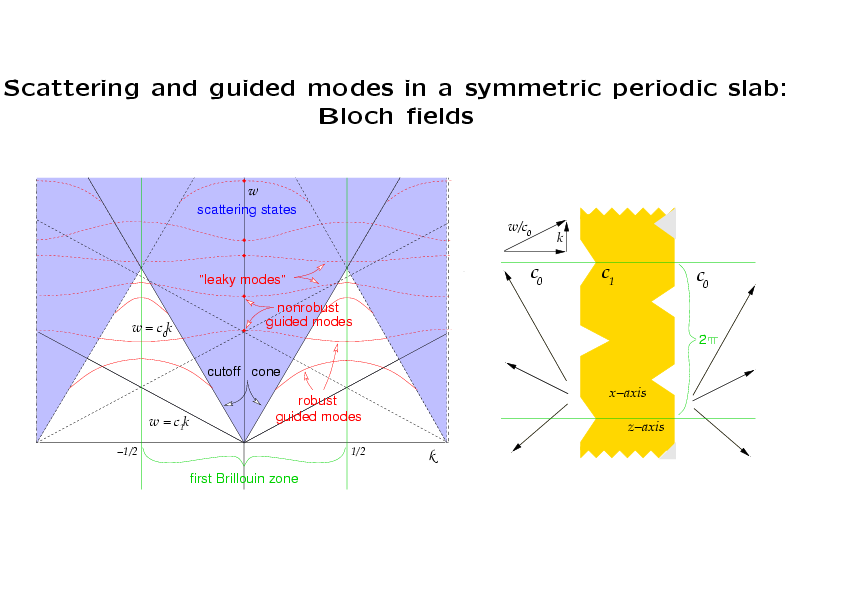
If the slab is symmetric about a horizontal line, then, for k=0, solutions can be decomposed into symmetric and antisymmetric parts. If, in addition, there is only one propagating harmonic (meaning that (k,ω) is in the blue diamond shape bounded by the cutoff cone and the dotted lines above it), then this propagating harmonic, which is symmetric, vanishes for antisymmetric solutions. Thus, if anitsymmetric solutions exist, they will be guided modes. In fact, one can prove that they do exist. They correspond to points on the complex dispersion relation where ω happens to be real; their frequencies are indicated by solid red dots on the graph. Since a perturbation of k results in a small imaginary part of ω, the guide mode is seen to disappear, and we call it nonrobust.

This is an instance of the disppearance of an eigenvalue embedded in the continuous spectrum of the Helmholtz operator with pseudo-periodic boundary conditions in the strip (0,2π)x(-∞,∞), where the parameter of perturbation is the pseudo-periodic factor e^2πik.

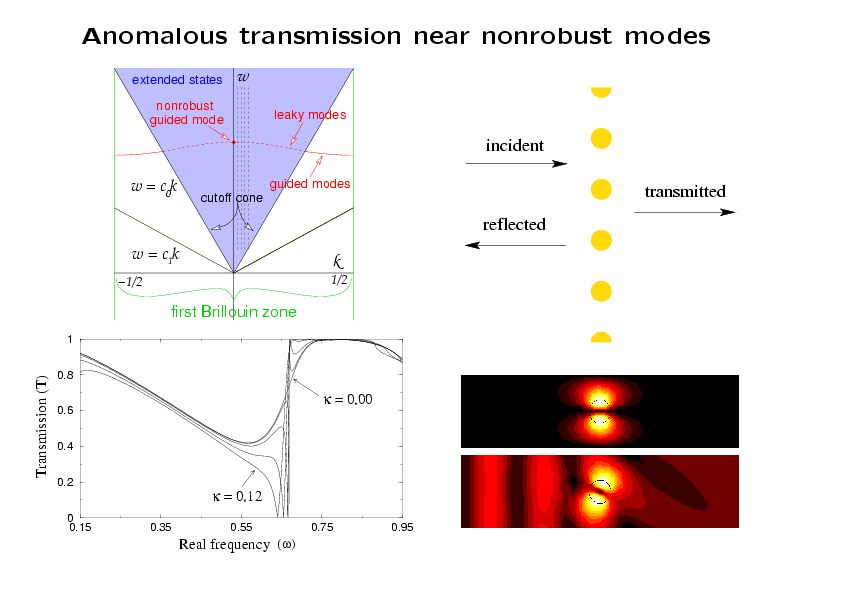
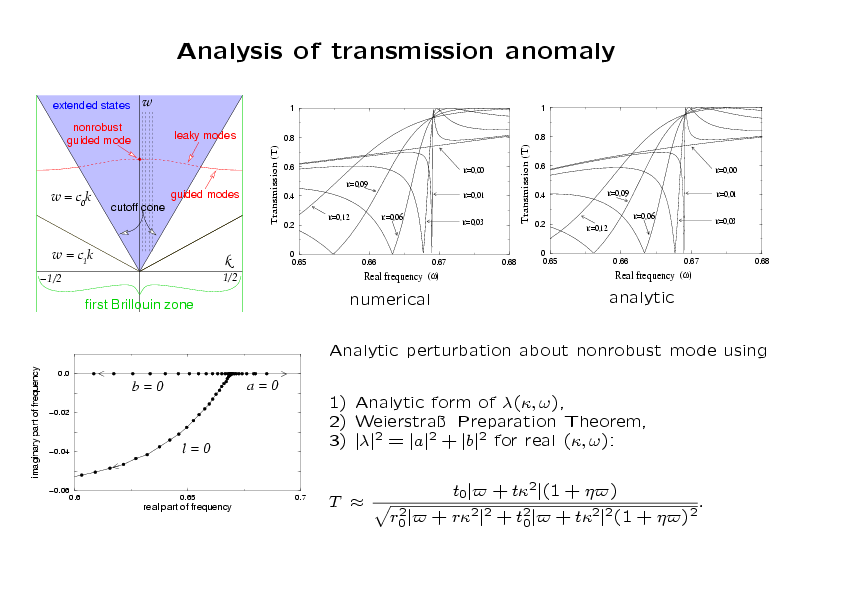
Numerical calculations of scattering by the yellow structure consisting of an infinite row of rods (seen in cross-section) demonstrate that a nonrobust guided mode produces anomalous transmission behavior. The structure admits a nonrobust guided mode at k = 0 and ω = ω₀ ≈ 0.667 (actually a standing mode because k=0). The transmission coefficient has been calculated numerically for frequencies from 0.15 to 0.95 for several values of k between 0.0 and 0.12. These intervals are shown by dotted vertical lines in the (k,ω)-plane, and the transmission is plotted in the lower left (a zoomed-in plot is shown several panels below.) At k = 0, there is no anomaly.

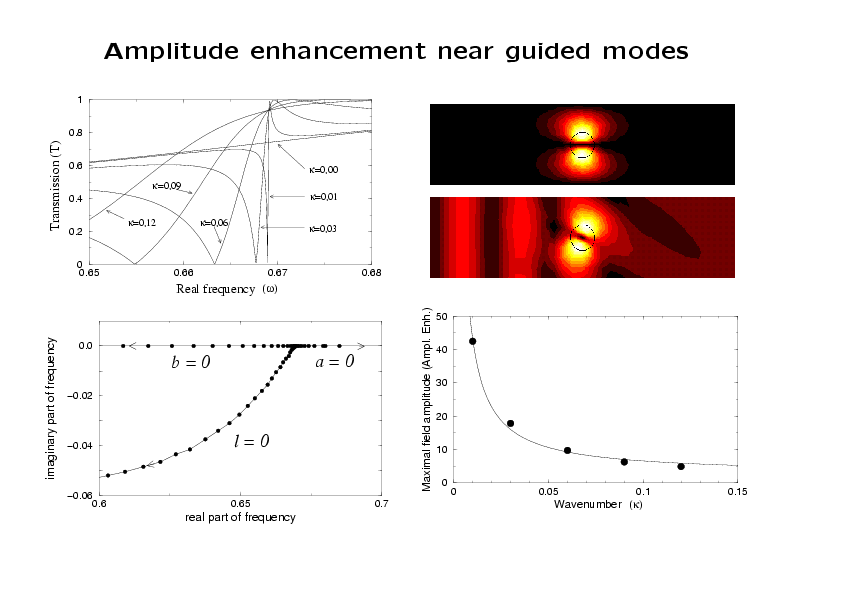
In the lower right, one period of the intensity of the guided mode is shown, and, below that, a field scattered by an incident wave from the left at a small nonzero value of k and a frequency near ω₀. This demonstrates the amplitude enhancement of fields due to resonant scattering near the guided mode parameters.

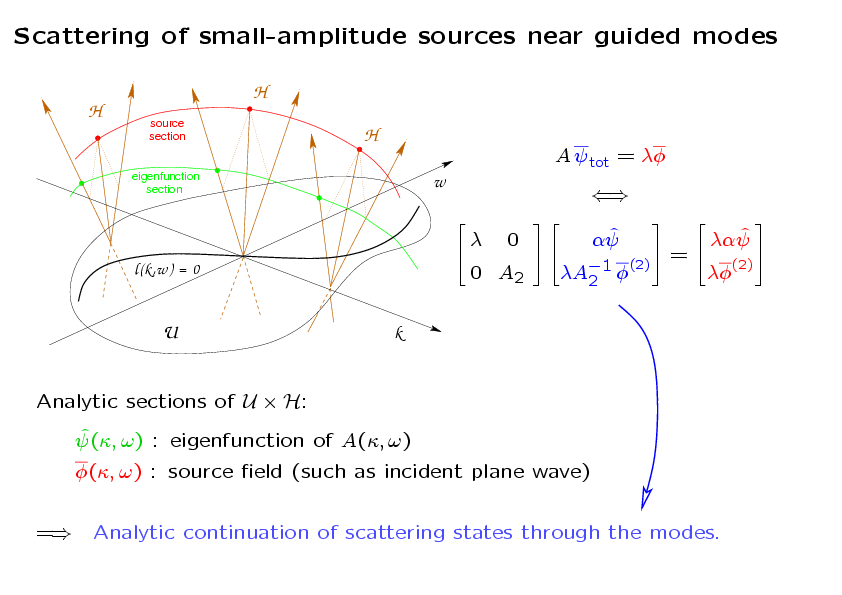
The scattering problem can be expressed in terms of values and normal derivative of the source and total (or scattered) fields on the air-slab interface in one period cell (in this case, over the boundary of one circlular cross section of a rod). These boundary data are called the traces of the fields. The total field trace is decomposed in a unique way into the traces of the source and scattered field exterior to the rod and in a (different) unique way into the source and scattered field interior to the rod. These decompositions are the images of the Calderón boundary projectors corresponding to the Green functions for the exterior and interior Helmholtz equations. The matrix Γ enforces matching conditions across the interface (typically Γ=I or Γ=diag(1,ν), where η gives the multiplicative jump in the normal derivative). The sum of the two projectors is I (they are complementary) if the air and slab have the same material properties. Otherwise, one shows the sum is of the form B+C, where B is bounded and C is compact.

This is what the boundary-integral equations look like. The exterior (radiating) and interior Green functions are denoted by G₀ and G₁.