Return to course home page
Math 4005: Geometry
The Sea Island Mathematical Manual
Introduction. The Sea Island Mathematical Manual (Haidao
Suanjing, 
) was
composed
in A.D.263 by the Chinese scholar-official Liu
Hui (
).
Originally, it was part of a commentary on an earleir mathematical work, the Jiuzhang
Suanshu, or The Nine Chapters on the Mathematical Art, an official
handbook used by the ruling civil bureaucracy. Liu felt that
the
treatment
of
certain
surveying
problems
was
inadequate. Therefore, he composed nine problems of his own and described
how to solve them.
Each problem
involved measurement of
distant
or
inaccessible
objects by triangulation.
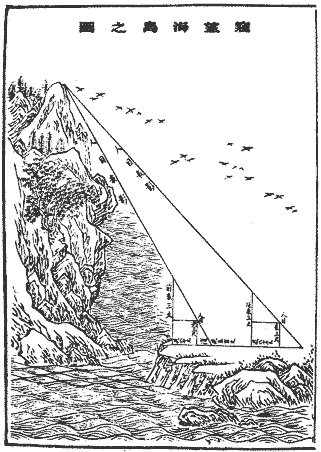
Liu's work was
made into a separate manual early in the Tang dynasty
(A.D. 618-906),
and it became part of the curriculum of study in the Chinese Royal Academy
in A.D. 656.
The title of the manual comes from the first problem, which is to measure
the height
of
a
peak
on
an
off-shore
island. A translation extensive information about
Liu's work can be found in: Swetz,
F.
(1992)."The
Sea
Island
Mathematical
Manual":
Surveying and Mathematics in Ancient China. University Park: The Pennsylvania
State University
Press 1992.
The problem.
The first problem in the Sea Island Mathematical
Manual is as follows. (The translation is quoted
from from Swetz, op. cit.)
Now for [the purpose of] looking at a sea island, erect two poles of the same
height, 3 zhang [on the ground], the distance between the front and rear [pole]
being a thousand bu. Assume that the rear pole is aligned with the front
pole. Move away 123 bu from the front pole and observe the peak of the island
from ground level; it is seen that the tip of the front pole coincides with
the peak. Move backward 127 bu from the rear pole and observe the peak of the
island from ground level again; the tip of the back pole also coincides with
the peak.
What is the height of the island and how far is it from the pole?
Comments. The diagram below shows the basic set-up of the Sea Island
problem. Lines that appear parallel are parallel. Point A is the top of
a mountain on an island out at sea. Point C is at sea-level, directly below
A. A surveyor on the mainland (DG) wishes to determine the height of the
mountain |CA|. However, she cannot get to any of the points A, B or C.
At best, she can find the distances between points in the set, {D, E, F,
G, H, I, J, K}.
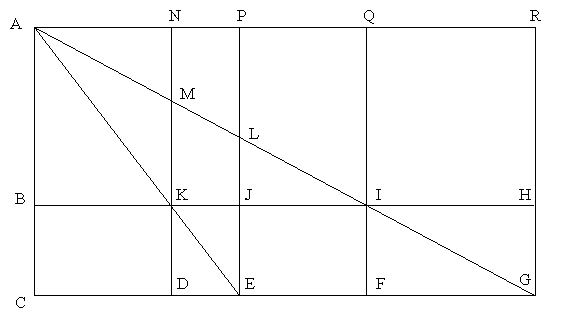
Problem. In the diagram above, suppose |KD| = 5, |DE| = 4,
|DF| = 12 and |DG| = 28. What is |AC|?
The following questions are intended as scaffolding to take you deeper into
this problem.
- What angles in the above figure are congruent? What triangles are similar?
What proportions are implicit in the diagram?
- Suppose lengths |KD|, |DE|, |DF| and |DG| are known. How can you use
this information to determine |AC|?
- There are numerous procedures that one might follow to compute |AC|
from measurements you might make between points whose names appear in the
INSIDE
the large rectangle. Challenge: describe as many different methods
as you can.
- Is it not necessary to know all the measurements listed in the previous
question in order to calculate |AC|. Suppose you can measure between
any two points whose names appear in the INSIDE the large rectangle. What
would
be the least number of measurements needed in order to provide enough
data to find |AC|? What would be the easiest procedure?
- Suppose you know
the ratio of |KI| to |EG| and the length |IF|. Can you find |AC|? Explain.