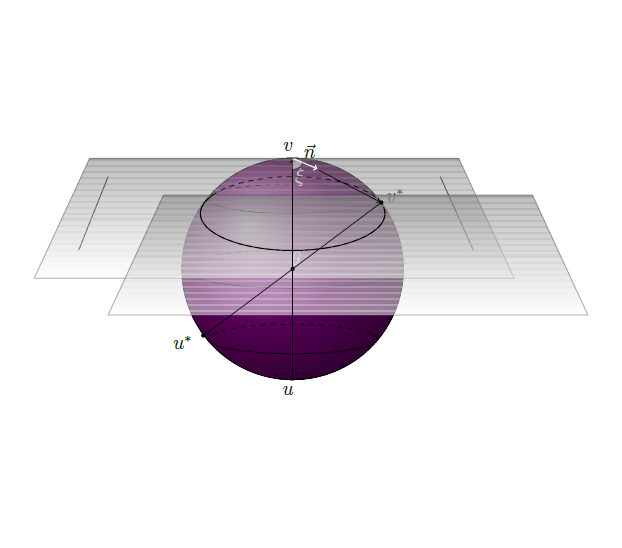
This years contest logo was developed by Professor Padmanabhan Sundar of the LSU Mathematics Department. The logo design gives a three-dimensional picture of collision dynamics of two colliding particles that travel in a vacuum. Here, \(u\) and \(v\) denote pre-collision velocities, and \(u^*\) and \(v^*\), post-collision velocities. On account of conservation of momentum and energy, they lie on a sphere with center at \(\frac{(u + v)}{2}\) and diameter equal to \( |v - u| \). One may take \(u\) as the south pole and \(v\) as the north pole. While the conservation laws provide us with four equations, \( (u^*, v^*) \) is six dimensional. Hence, in writing \(u^*\) and \(v^*\) as functions of \(u\) and \(v\), one needs two parameters. If the unit vector in the direction of \(v^* - v\) is called \(n\), then it enables one to write \(v^*\) in terms of \(u\), \(v\) and \(n\). In spherical coordinates, \(n\) is written as a function of \(\theta\) and \(\xi\) where \(\theta\) is the co-lattitude and \(\xi\) is the meridian for the velocity \(v^*\).