|
We owe the drawing of the T-shirt design and our 2005 contest
logo to professor Larry Smolinsky from LSU Math Department.
It portrays a covering space.
A covering map is a continous onto map
p : C  X
X
with C and X being topological spaces,
which has the following property:
- to every x in X there exists an open
neighborhood U such that p -1(U)
is a union of mutually disjoint open sets U~i
(where i ranges over some index set I)
such that p restricted to U~i
yields a homeomorphism from U~i
to U for every i in I.
We say C is a covering space
of X.
Our 2005 contest logo portrays a complicated case of
a covering space C. We will try to explain here a simpler
example.
 |
 |
 |
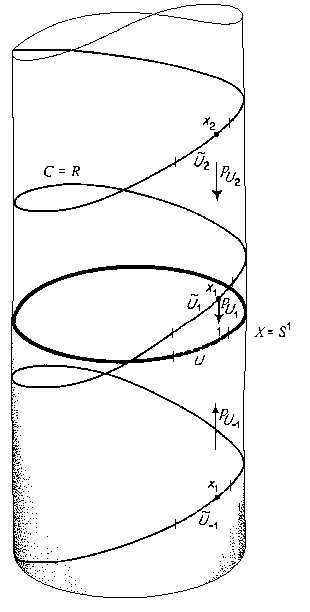
| On the picture above C = R
is potrayed as a spiral around a vertical cylinder,
and X = S1 lies in
a horizontal plane perpendicular to the axis of the
cylinder. |
Consider X being the unit circle S1
in R2.
Then the map
p : R  S1
S1
with
- p(t) = (cos(t),sin(t))
is a covering map, and C = R
is a covering space of X = S1.
In this case C = R
can be drawn as a spiral:

The picture on the right explains the details.
|