We owe the T-shirt design and our 2014 contest logo design to Prof. Gestur Olafsson of LSU Math Department. We also thank Richard Frnka who created the electronic files.

The sphere \( \mathrm{S}^n=\{\mathbf{v}\in \mathbb{R}^{n+1}\mid \|\mathbf{v}\|=1\}\) is a closed compact manifold in \(\mathbb{R}^{n+1}\). It is well know that polar-coordinates play an important role in analysis on \(\mathbb{R}^{n+1}\), in particular, in solutions of differential equations with rotational symmetry. One can also define polar coordinates on the sphere. For that we embed \(\mathrm{S}^{n}\) into \(\mathrm{S}^{n+1}\) by \(\mathbf{u}\mapsto (0,\mathbf{u})\). If \(\mathbf{v}\in \mathrm{S}^n\) then we write \(\mathbf{v}=(x_1,\mathbf{x})\) with \(\mathbf{x}\in \mathbb{R}^n\). 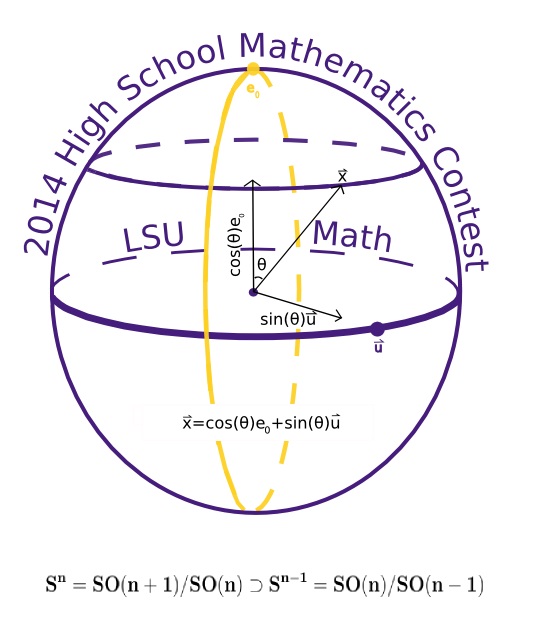As \(\|\mathbf{v}\|=1\) it follows that \(x_1^2+\|\mathbf{x}\|^2=1\). We can therefore write \(x_1=\cos (t)\) and \(\|\mathbf{x}\|=\sin (t)\) for some \(t\in [0,\pi]\). If \(\mathbf{x}\ne\mathbf{o}\) then \(\mathbf{u}=(1/\sin t)\, \mathbf{x}\in \mathrm{S}^{n-1}\) and \(\mathbf{v}=\cos (t)\mathbf{e}_1+\sin (t) \mathbf{u}\) where \(\mathbf{e}_1=(1,0,\ldots ,0)^t\) is the first standard basic vector for \(\mathrm{R}^{n+1}\). The coordinates \((t,\mathbf{u})\in (0,\pi)\times \mathrm{S}^{n-1}\) are the polar-coordinates for the sphere. \[\] The sphere is an example of a homogeneous manifold. Denote by \(\mathrm{GL} (n+1,\mathbb{R})\) the group of all invertible \((n+1)\)-matrices. The special orthogonal group \(\mathrm{SO} (n+1)\) is defined by \[\mathrm{SO} (n+1)=\{A\in \mathrm{GL} (n+1,\mathbb{R})\mid (\forall \mathbf{v},\mathbf{w}\in\mathbb{R}^{n+1})\, \langle A\,\mathbf{v} ,A\,\mathbf{w} \rangle =\langle \mathbf{v} , \mathbf{w}\rangle \text{ and } \det A=1\}\, .\] If \(\mathbf{v}\in \mathrm{S}^n\) then we also have \(\|A\,\mathbf{v}\|=1\) and hence \(A\, \mathbf{v}\in \mathrm{S}^n\). Write \(A=[\mathbf{a}_1,\ldots , \mathbf{a}_{n+1}]\) where \(\mathbf{a}_1,\ldots ,\mathbf{a}_{n+1}\) are column vectors. We have \(A\,\mathbf{e}_1=\mathbf{a}_1\). On the other hand, if \(\mathbf{v}\in\mathrm{S}^{n}\) then we can extend \(\mathbf{a}_1=\mathbf{v}\) to a positively oriented orthonormal basis \(\mathbf{a}_1,\ldots ,\mathbf{a}_{n+1}\) of \(\mathbb{R}^{n+1}\). Then \(A=[\mathbf{a}_1,\ldots ,\mathbf{a}_{n+1}]\in\mathrm{SO} (n+1)\) and \(A\,\mathbf{e}_1=\mathbf{v}\). The group that fixes the ''north pole'' \(\mathbf{e}_1\) is the group \(\mathrm{SO} (n)\) and hence \(\mathrm{S}^{n}\simeq \mathrm{SO} (n+1)/\mathrm{SO} (n)\) where the isomorphism is given by \(A/\mathrm{SO} (n)\mapsto A\mathbf{e}_1\).