Introduction to Mathematical Modeling for Liquid Crystals
Liquid crystals (LCs) are an awesome material with interesting physics and applications such as LCDs (read more about LCs on Wikipedia).
Nematic LC molecules look like elongated rods:


The orientation of the molecules affects the material's behavior, especially optical properties such as birefringence:


which make LCs useful for Liquid Crystal Displays (LCDs).
We can model (at the macroscopic level) the orientation of LC molecules by an arrow called the director:
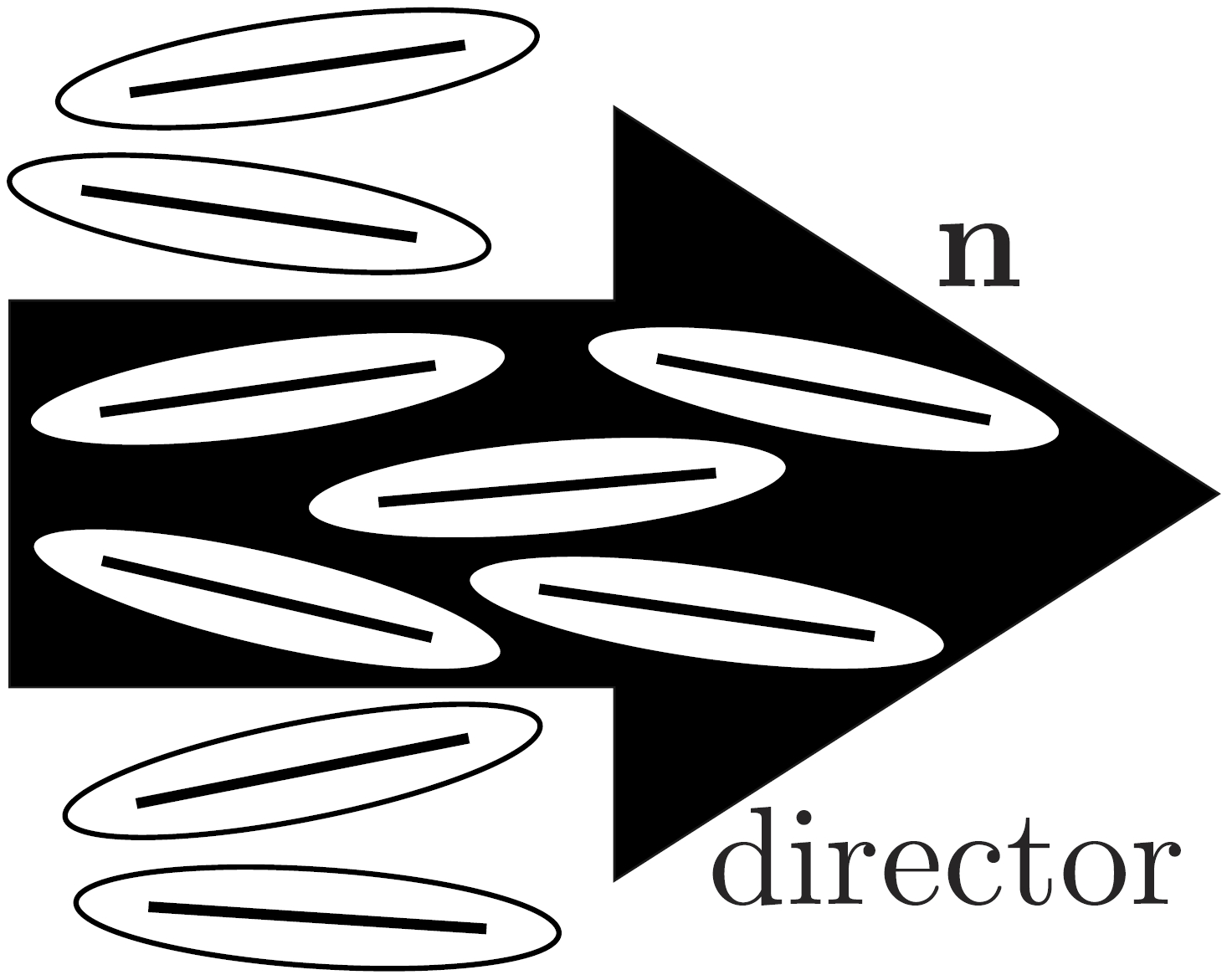
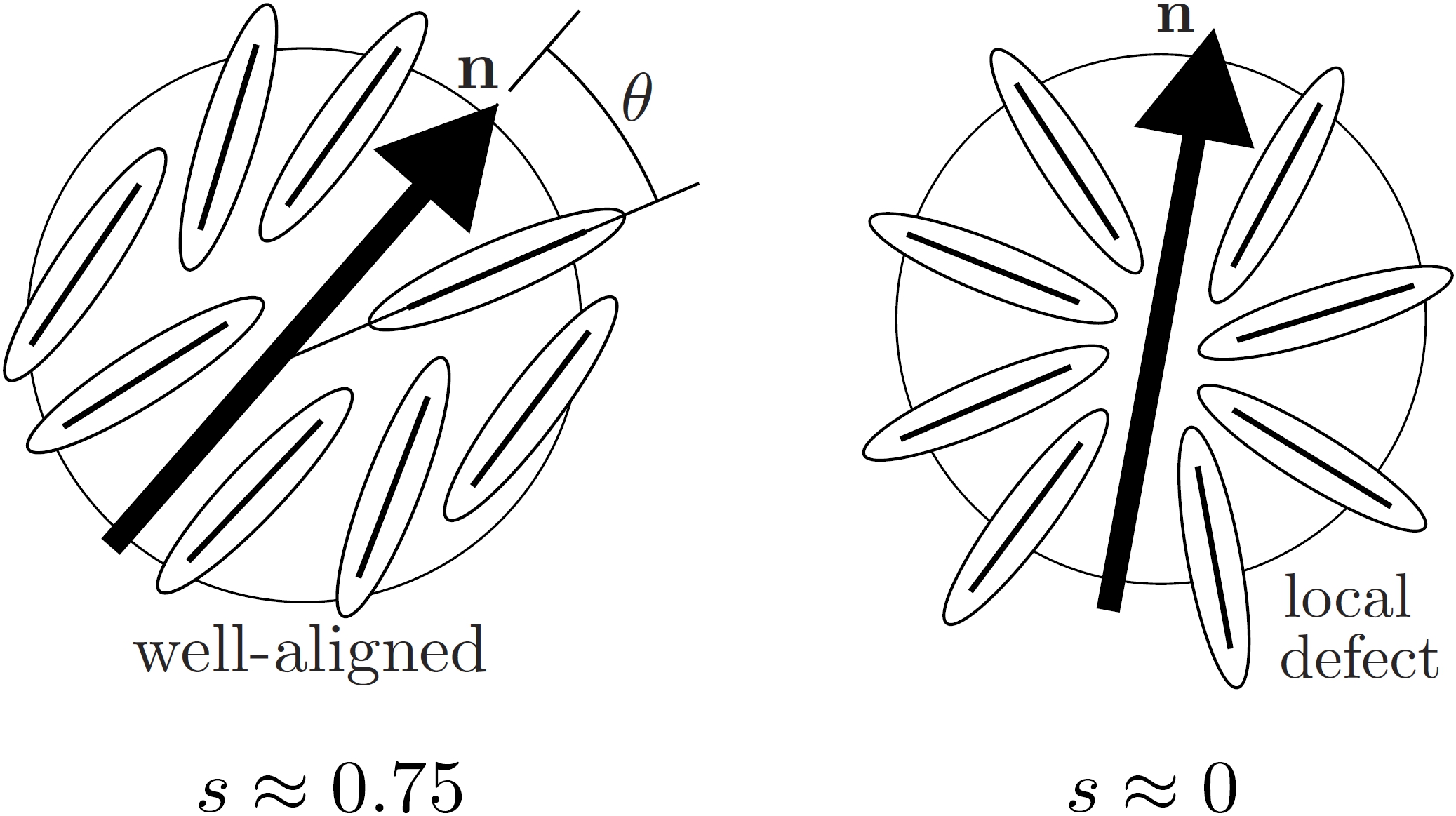
Actually, we use a vector field (lots of little arrows) to represent the orientation of lots of LC molecules (see the simulation figures below). And we can model the "degree of orientation" (how well aligned the molecules are) by a scalar order parameter "s".
The following papers describe a particular model and numerical method to simulate the equilibrium state of liquid crystals:
Numerics for Liquid Crystals with Variable Degree of Orientation
MRS proceedings, Symposium NN – Math. and Comp. Aspects of Mater. Sci., vol. 1753, 2015.
A Finite Element Method For Nematic Liquid Crystals With Variable Degree Of Orientation
SIAM Journal on Numerical Analysis, vol 55, no 3, pg 1357-1386, June 2017.
The Ericksen Model of Liquid Crystals with Colloidal and Electric Effects
Journal of Computational Physics, vol 352, pg 568 - 601, 2018.
A Coupled Ericksen/Allen-Cahn Model For Liquid Crystal Droplets
Computers & Mathematics with Applications, vol 75, no 11, pg 4048 - 4065, 2018.
A Finite Element Method for a Phase Field Model of Nematic Liquid Crystal Droplets
Communications in Computational Physics, vol 25, pg 155-188, 2019.
A Finite Element Method for the Generalized Ericksen Model of Nematic Liquid Crystals,
in review.
This music video provides a summary of our earlier work on the Ericksen model (vimeo link).
Music "Undertow" by Duff Paulsen used with permission.
See below for more simulations and pictures.
Simulations of the Ericksen Model
Here are simulations showing the evolution of a liquid crystal director field toward equilibrium using our provably robust gradient flow scheme.
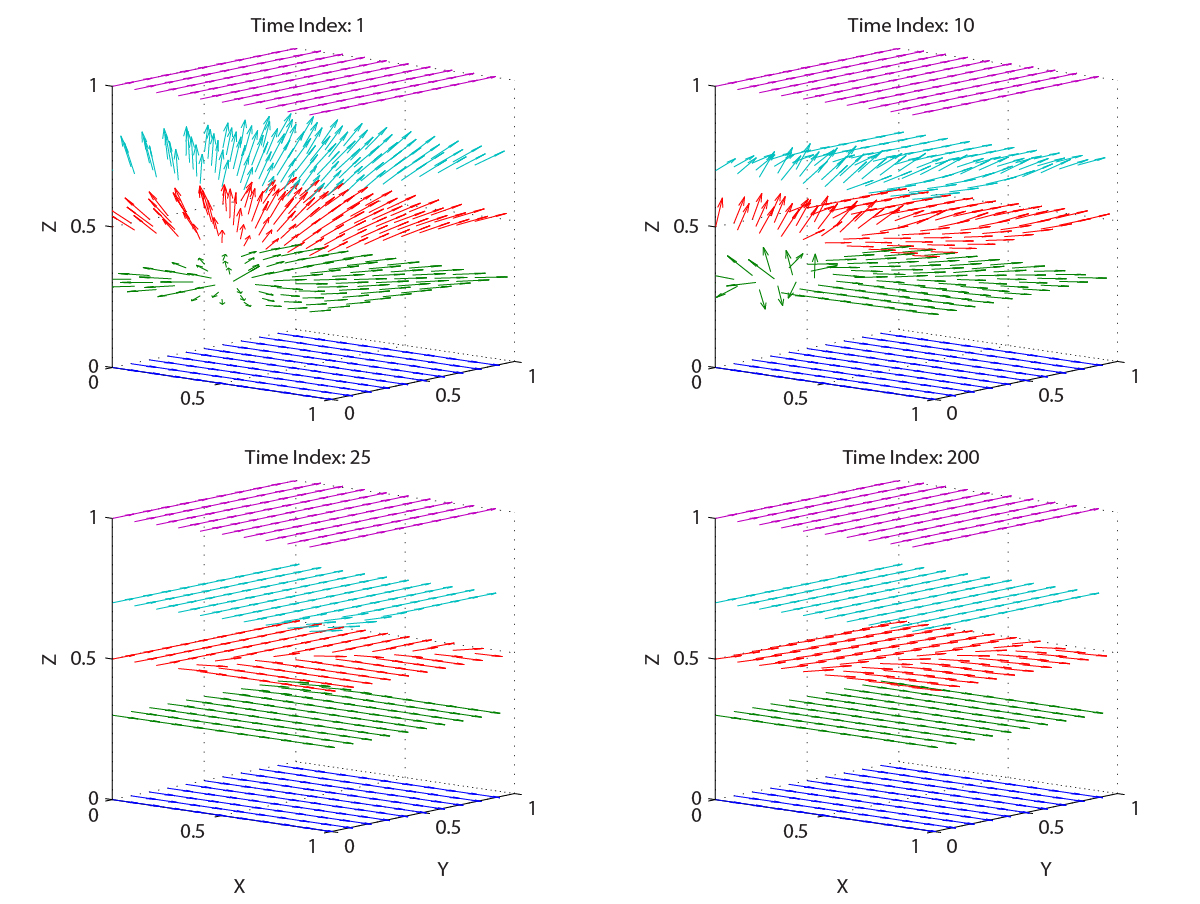
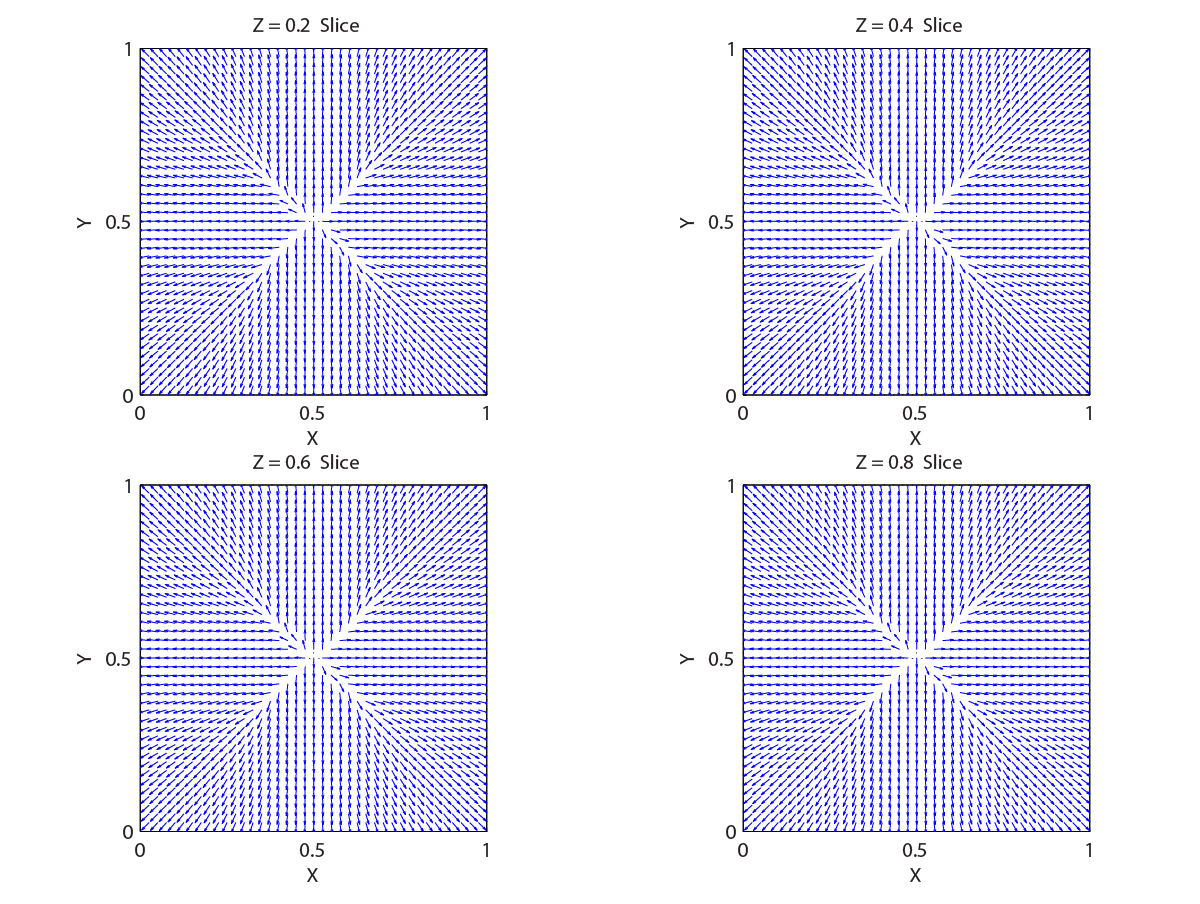
- Plane Defect in 3-D. The equilibrium configuration has a discontinuity in the director field at z = 0.5. Figure above shows horizontal slices of the director field at four "time" instances of the gradient flow scheme. Near the bottom, the director points along the x direction; near the top, the director points along the y direction.
- Windmill Defect in 3-D. The equilibrium configuration has an "X" shaped discontinuity in the director field. Figure above shows different cross-sections (parallel to the x-y plane) to illustrate the defect at the last iteration of the gradient flow scheme.
Simulations of the Uniaxially Constrained Landau-de Gennes Model
We have extended our method for the Ericksen model to simulate the Landau-de Gennes Model with a uniaxial constraint imposed on the order parameter Q.
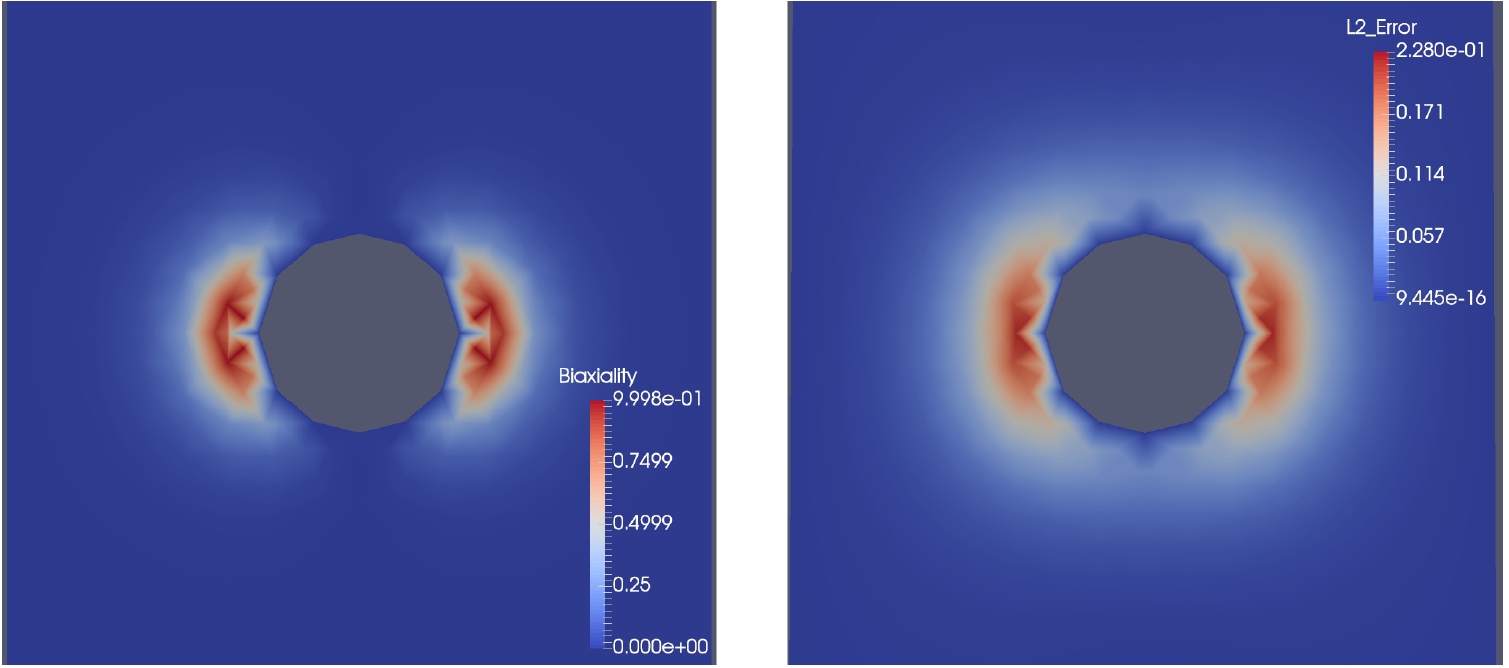
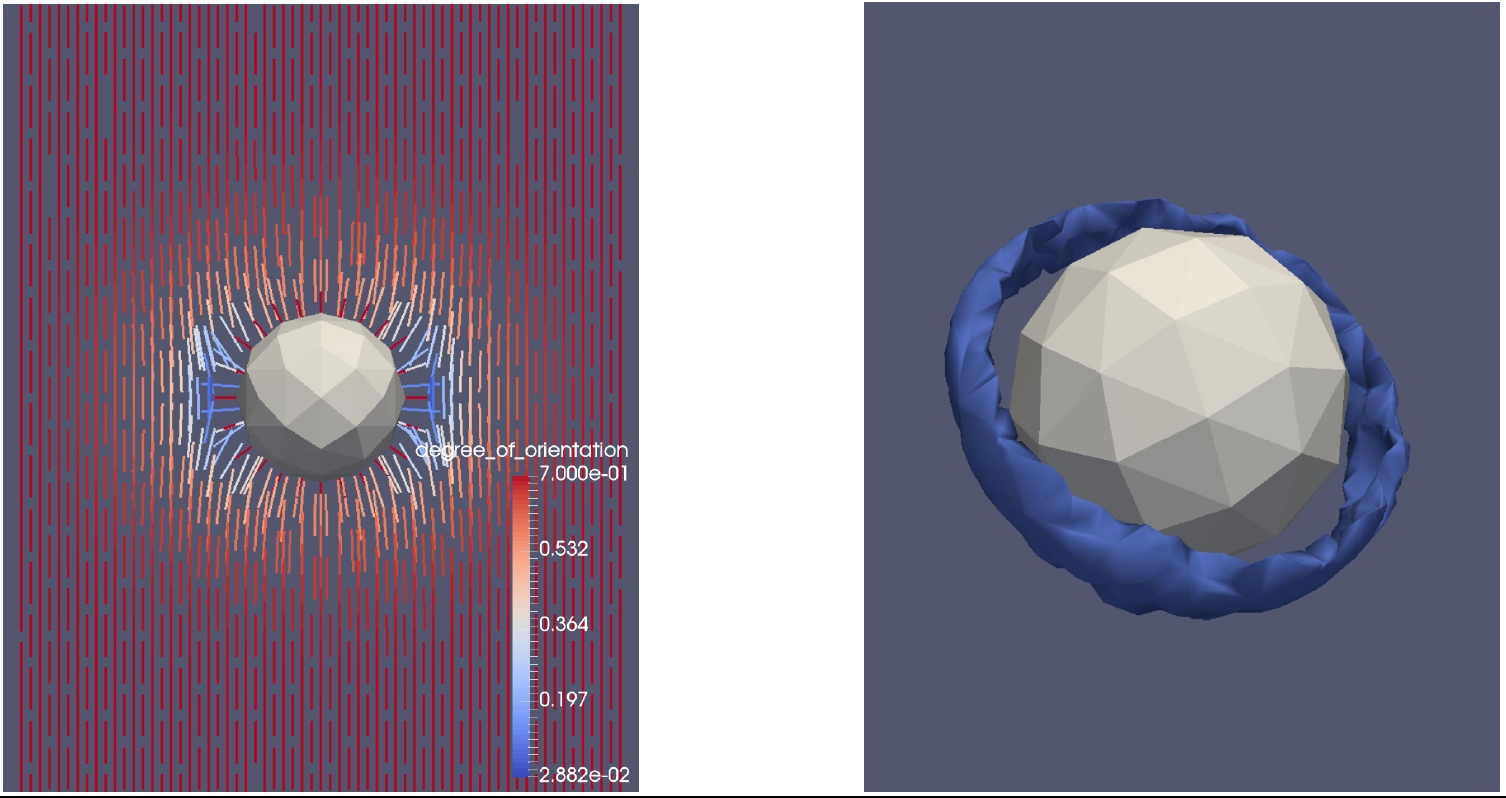
- Visualization of the uniaxial LdG solution with Saturn-ring defect. Left: cross-section view of line-field (headless director field); the -1/2 degree defect (discontinuity) is clearly visible on the left and right sides of the hole. Right: the Saturn-ring defect depicted as the s=0.11 iso-surface.
- Comparison of standard LdG with uniaxially constrained version, using the Saturn-ring defect as example. Left: the "standard" one-constant LdG model exhibits maximum "biaxiality" at the defect. Right: the pointwise L2 error between the minimizer from the standard model and the minimizer with uniaxial constraint.