| |
Links:
Math Department
LSU Home Page
Am. Math Soc.
Math. Assoc. Am.
Nat. Sci. Found.
Siblinks:
Barbara
Michael
Patrick
Art
Birds
|
|
|

Undergraduate Research Experiences
Waves, trapped energy, and resonance in combinatorial and quantum graphs provide and excellent medium for research projects for undergraduate mathematics students at all levels. The subject touches many areas of mathematics, such as partial and ordinary differential equations, linear and nonlinear algebra, Fourier analysis, geometry, operators, and spectral theory, and benefits from a rich ideological symbiosis with phenomena of physics.
Over the years, I have worked with many undergraduate students in summer REUs, vertically integrated courses, and honor theses, on projects involving waves and resonance in graphs. Below are links to descriptions of some of these projects and posters created by students.
2022 Discover Day and Spring TX-LA Undergraduate Mathematics Conference
- Free Oscillations of Coupled Strings, by Lillian Powell
2019 TX-LA Undergraduate Mathematics Conference
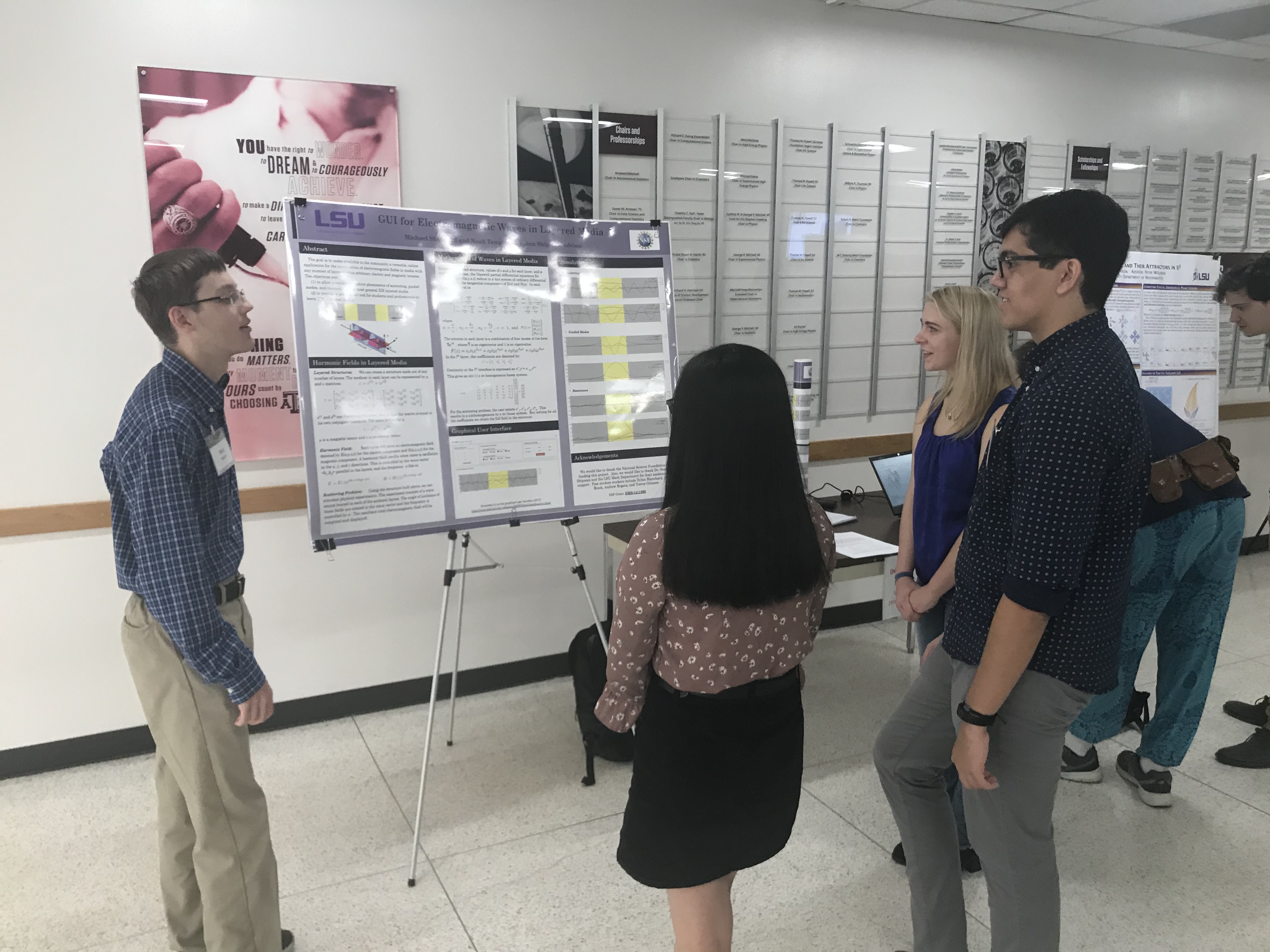
- An Online GUI for EM Waves in Layered Media, by Noah Templet and Michael Sheppard
2017 LSU Discover Day
- Toy Model for Density of Bound States, by Stacey Wieseneck
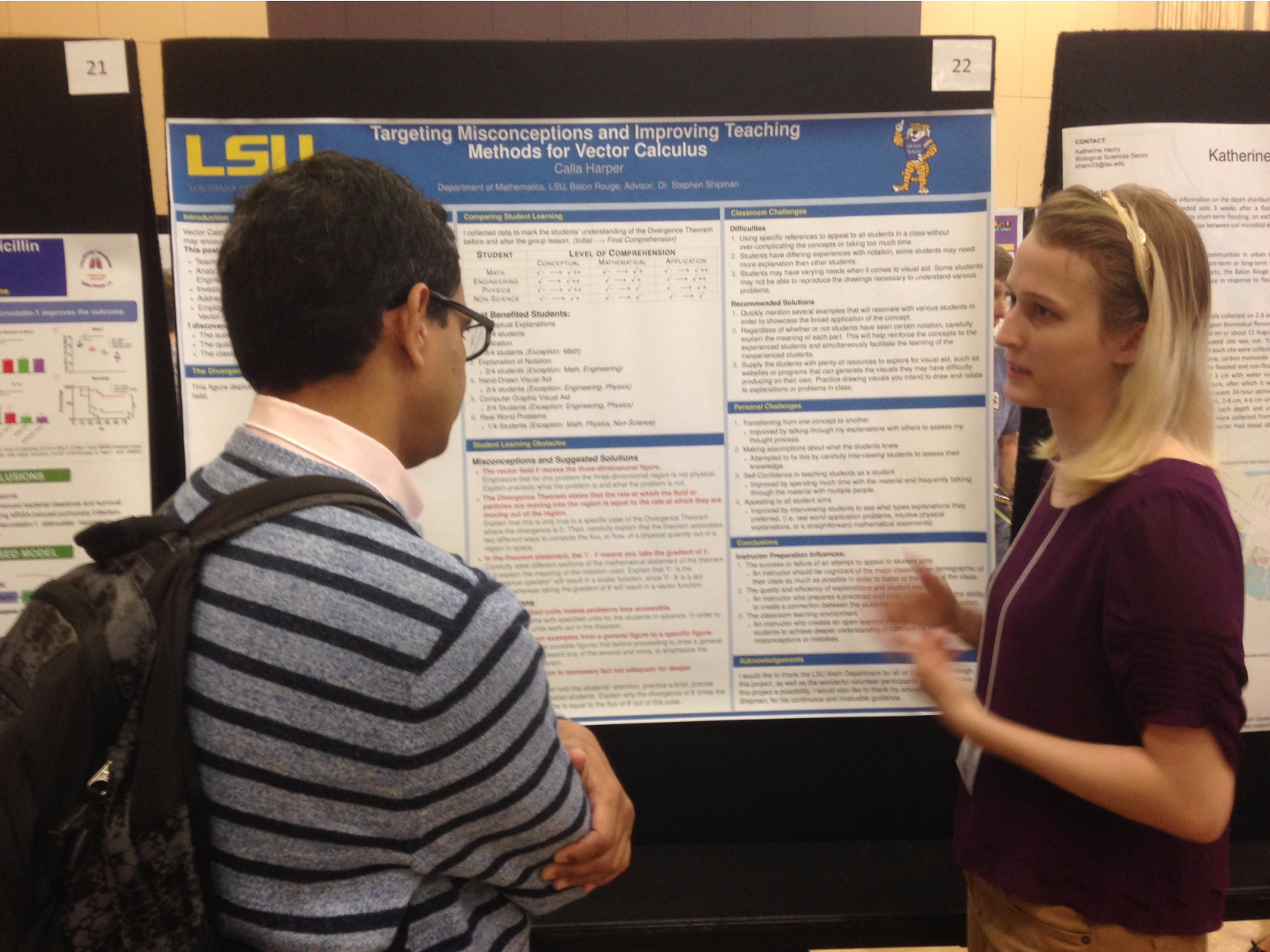
- Targeting Misconceptions and Improving Teaching of Vector Calculus, by Calla Harper
2014 Summer Group on Quantum Graphs
- Spectra of Quantum Binary Trees, by Alexa Martin
- Effects of Structure on Spectra of Periodic Quantum Graphs, by Michelle Laskowski
- Waves in a String with Decaying Defect Density, by Melanie Dutel and Morgan Landry
2012 Fall VIGRE Course on Resonance
- Polarization Rotation on a Complex Scatterer,
by Jeremy Baumgartner, Patrick Keiffer, and Jerome Weston
- Guided Modes and Resonance in Anisotropic Media,
by Laura Johnson, Joe Poynot, and Andrew Rogers
- Resonance on a Line Defect in a 2D Lattice,
by Emelie Mativi, Tyler Meyer, Ian Runnels, and Jeremy Tillay
- Resonant Behavior in Embedded Impurity Bands,
by Christina Davis, Dominique Gautreau, Charles Stephens, and Andrew Williamson
2012 Summer Group on Resonance in Lattices
- Resonance Between Bound States and Radiation in Lattices, by Jeremy Tillay
- A Lattice Model for Optical Resonance, by Emelie Mativi
- Resonant Frequency Selection in a Lattice, by Grace Silaban
- A Lattice Model for Metamaterials, by Tyler Meyer
2009 High School Math Circle Project
- Oscillations in a Chain of Beads, by Hira Kahn and Joyce Ward
2009 Spring VIGRE Course on Wave Scattering
- Resonant Scattering by an Open Waveguide: Dependence on Angle of Incidence and Geometry,
by Jennifer Ribbeck, Katherine Smith, and Clayton Weeks
- Modification of Energy Transmission Through Periodic Rod Structures,
by Maliha Bahri, Jessica Dowd, Paul Faciane, and Steven LaRosa
2022 Discover Day and TX-LA Undergraduate Mathematics Conference
This project was presented at LSU's 2022 Discover Day and the Third Annual meeting of the TX-LA UG Math Conference.
Free Oscillations of Coupled Strings, by Lillian Powell
Supported by LSU President's Aid and NSF Award DMS-1814902.

|

|

|

|
|
Lillian is a mathematics and physics major at LSU.
She investigated the free oscillatory frequencies of system of strings coupled together at their ends and produced animations of the oscillating modes. The computations involve finding eigenvalues and eigenfunctions of a Schrödinger operator on a metric graph.
|
2019 TX-LA Undergraduate Mathematics Conference
This project was presented at the Third Annual meeting of this conference:
LINK.
An Online GUI for EM Waves in Layered Media, by Noah Templet and Michael Sheppard
Noah is a CS major and Michael is a math major at LSU.
2017 LSU Discover Day
In the spring of 2017, two students participated in Discover Day 2017 at LSU.
Toy Model for Density of Bound States, by Stacey Wieseneck
Stacey Wieseneck is a senior student of chemical engineering at LSU.
Targeting Misconceptions and Improving Teaching of Vector Calculus, by Calla Harper
Calla Harper is a senior mathematics major who is in the Geaux Teach program at LSU.
2014 Summer Group on Quantum Graphs
In the summer of 2014, four undergraduate students participated in a research group on quantum graphs. They presented three posters at LSU's SURF, the Summer Undergraduate Research Forum.
Spectra of Quantum Binary Trees, by Alexa Martin
Supported by NSF Robert Noyce Teacher Scholarship Program.
Alexa Martin is a mathematics major at LSU and participates in LSU's Geaux Teach program for mathematics teachers.
She investigated the vibrational frequencies of binary tree graphs. The spectrum of frequencies can be computed for a binary tree of any size n from the roots of a polynomial of degree n in the cosine of the frequency. These polynomials can be computed recursively in n as the determinant of an nxn matrix.
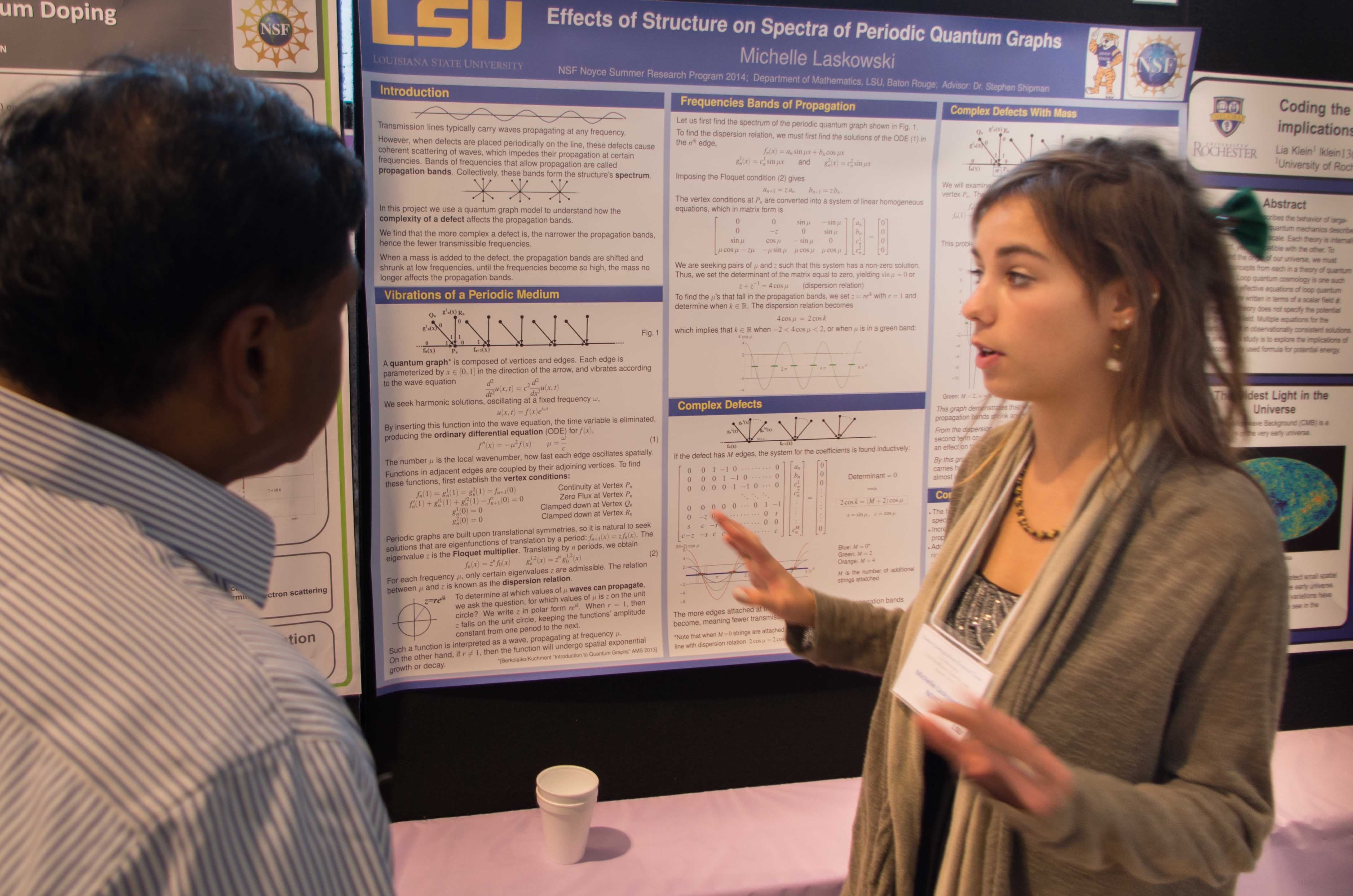
Effects of Structure on Spectra of Periodic Quantum Graphs, by Michelle Laskowski
Supported by NSF Robert Noyce Teacher Scholarship Program.
Michelle Laskowski is a mathematics major at LSU and participates in LSU's Geaux Teach program for mathematics teachers.
She investigated the band-gap structure of the spectrum of 1D-periodic quantum graphs and how the bands depend on the complexity of the cell structure.
Waves in a String with Decaying Defect Density, by Melanie Dutel and Morgan Landry
Supported by the LA Board of Regents Mathematics College Readiness and Retention Program and the NSF VIGRE program.
Melanie Dutel is a mathematics major at LSU; Morgan Landry is also a mathematics major and participates in LSU's Geaux Teach program for mathematics teachers. They investigated waves in a string with defects that are not regularly spaced. The problem is converted into a discrete dynamical system that exhibits initial exponential growth depending on the mass of the defects and fractal behavior.
2012 Summer Group on Resonance in Lattices
In the summer of 2012, four undergraduate students participated in a research group on lattice models of resonance phenomena in photonics. They presented four posters at LSU's SURF, the Summer Undergraduate Research Forum.
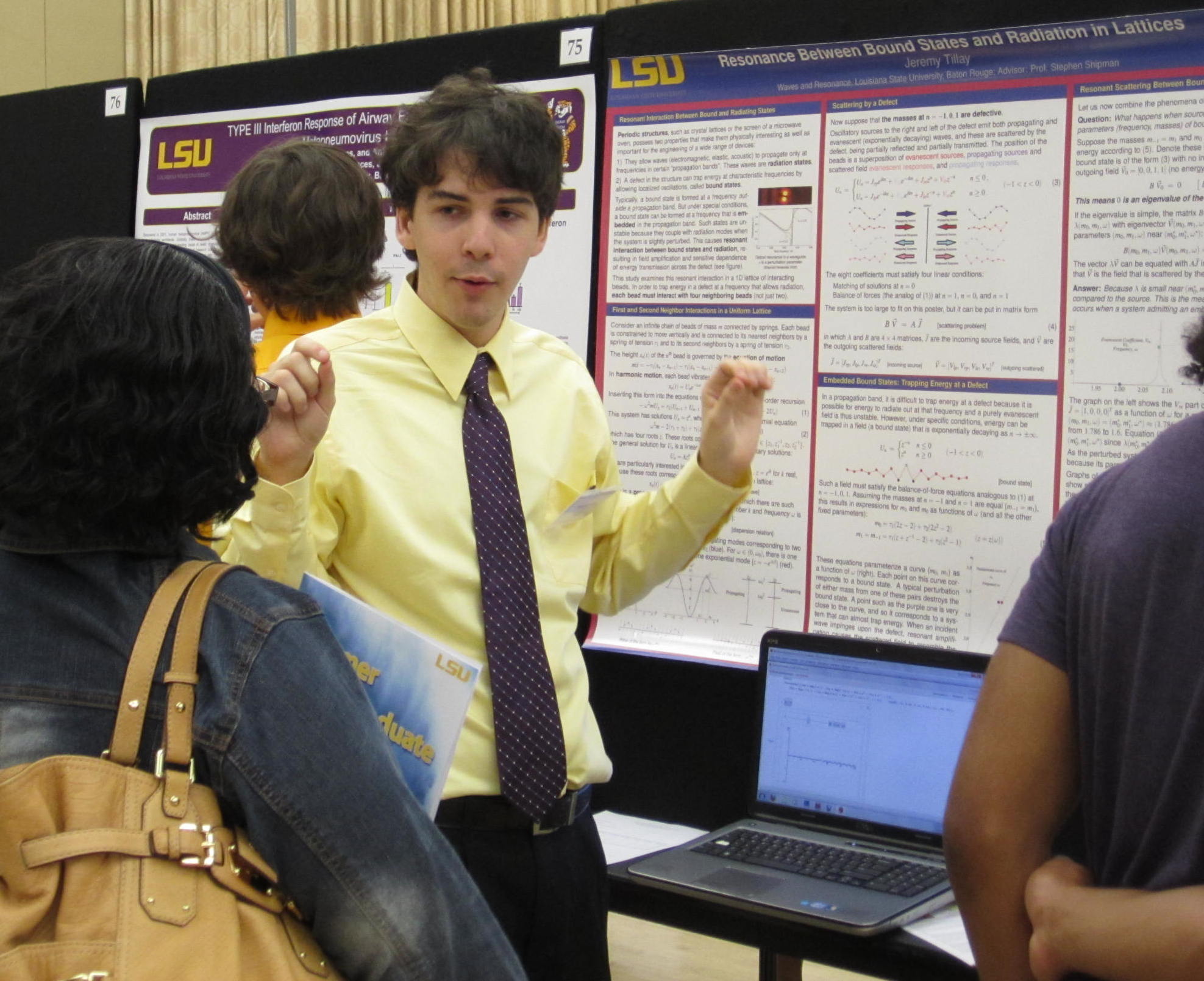
Resonance Between Bound States and Radiation in Lattices, by Jeremy Tillay
Supported by the LA-STEM Research Scholars Program at LSU.

|

|

|
|
|
Jeremy is a mathematics major at LSU.
He investigated a one-dimensional model of a discrete bimodal transmission line. In certain frequencies, one mode is propagating and the other is evanescent. This is made possible by next-nearest neighbor interactions between sites on the discrete line. A carefully chosen defect in the line allows energy to be trapped in the evanescent modes. A perturbation of this system instigates a resonant interaction between the propagating mode and the trapped-energy state.
|
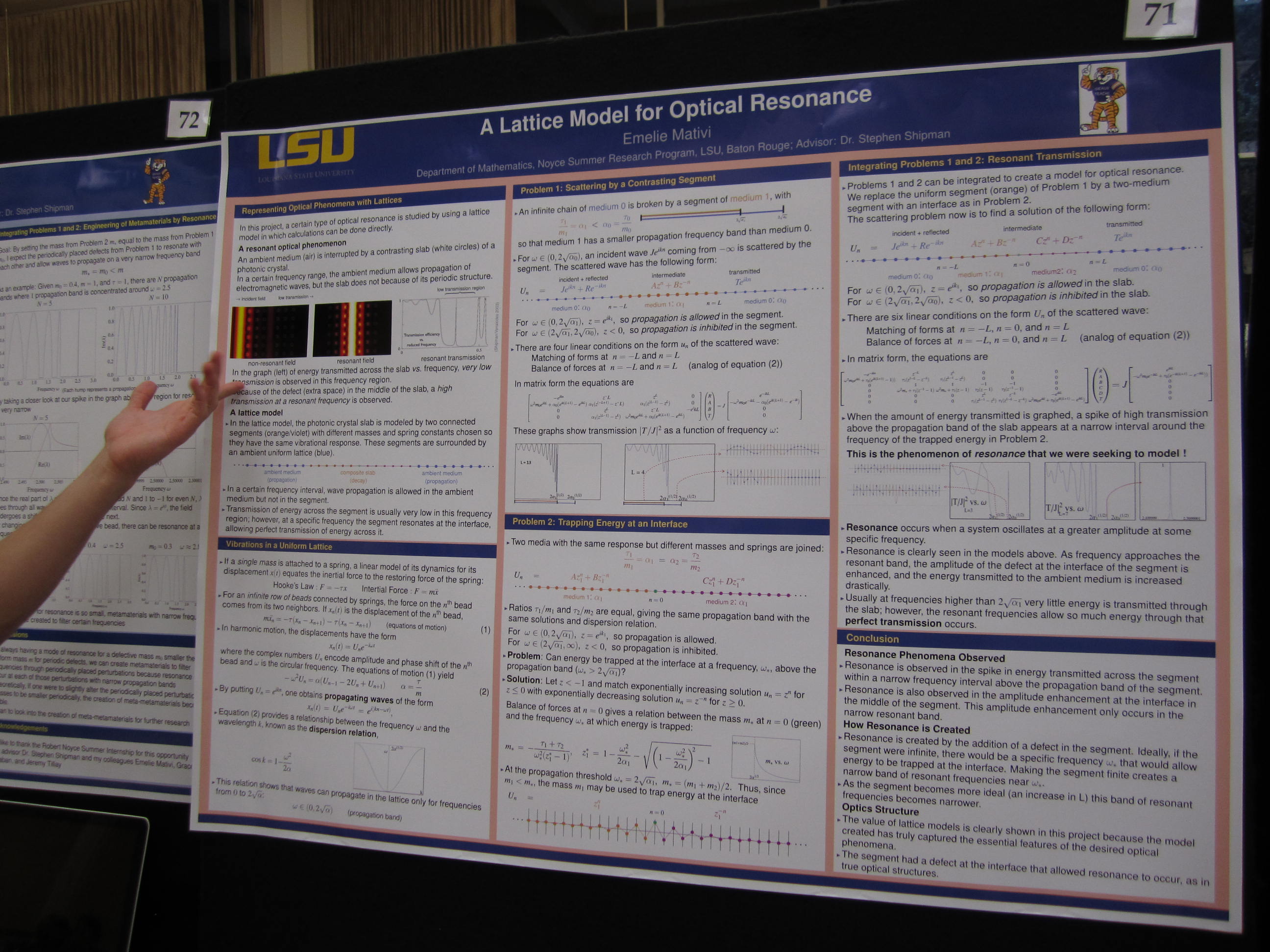
A Lattice Model for Optical Resonance, by Emelie Mativi
Supported by NSF Robert Noyce Teacher Scholarship Program.

|

|

|
|
|
Emelie is a mathematics major and participates in LSU's Geaux Teach program for math teachers.
She investigated a lattice model for a phenomenon in optics known as "Fabry Perot" resonance, in which an optical mode of a photonic crystal cavity is strongly excited by radiation modes that weakly penetrates into the cavity.
|
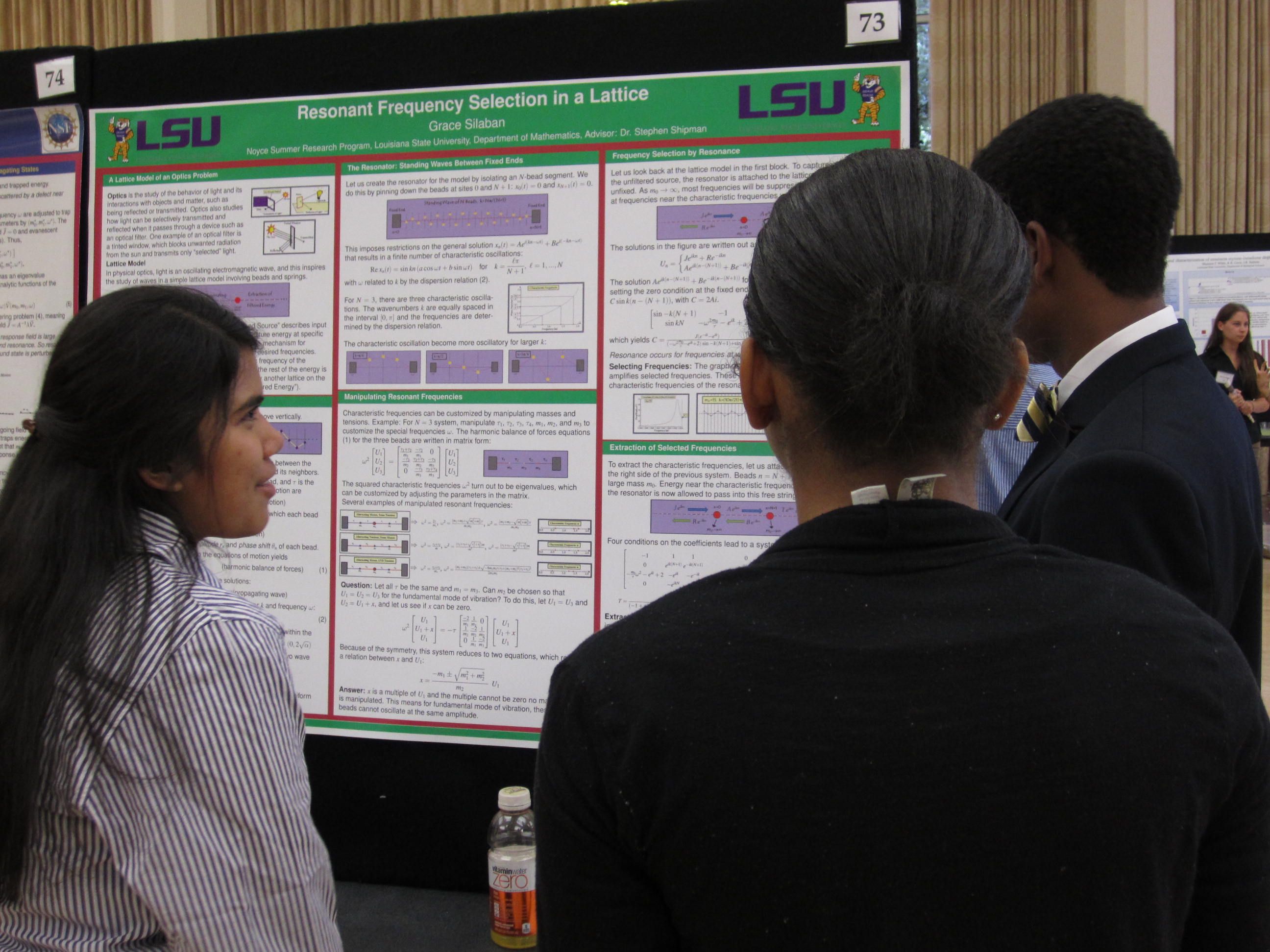
Resonant Frequency Selection in a Lattice, by Grace Silaban
Supported by NSF Robert Noyce Teacher Scholarship Program.

|

|

|
|
|
Grace is a mathematics major and participates in LSU's Geaux Teach program for math teachers.
She investigated a lattice model for optical frequency selection, or filtering, by exploiting a resonant cavity.
An unfiltered source field in an incoming transmission line strikes a resonant cavity, which captures energy at specifically tuned frequencies. An outgoing transmission line is excited a precisely these frequencies and therefore is able to extract, or filter, them for use in a frequency-specific device.
|
A Lattice Model for Metamaterials, by Tyler Meyer
Supported by NSF Robert Noyce Teacher Scholarship Program.

|

|

|

|
|
Tyler is a mathematics major and participates in LSU's Geaux Teach program for math teachers.
He investigated a lattice model for metamaterials. By tuning a periodically dispersed defect within a lattice host material, an isolated frequency band of propagation can be made to be arbitrarily narrow. This effectively creates a material that inhibits the propagation of waves at all frequencies of a source field and allow a single frequency to pass, or filter, through.
|
2009 Summer High School Math Circle
For the High School Math Circle in 2009, I presented a purely geometric way to construct the spectrum and trapped-energy modes for a simple one-dimensional lattice. Two students, Hira Khan and Joyce Ward, mentored by graduate student Rick Barnard, wrote an exposition of this problem and presented it in the last day of the Math Circle. The following fall semester, they travelled with a cohort from the LSU Mathematics Department to San Francisco to present their work in a Math Circle session of the joint meetings of the American Mathematical Society and the Mathematical Association of America.
|