Waves in Complex Media:

Scattering of Waves by Periodic Structures

Proceedings of the Course

Notes from the presentations by faculty and graduate students

	Stephen Shipman	Scattering by periodic structures
	Robert Lipton	Dido's problem and isoperimetric inequalities
	Alvaro Guevara	How to build a graphical user interface (GUI) in Matlab.
	Silvia Jimenez	Introduction to periodic homogenization
	Silvia Jimenez	Functional analysis for homogenization
	Hairui Tu	Boundary-integral methods in scattering
	Santiago Fortes	Dispersion relations for layered media with negative index
	Hai Ngo	Scattering by periodic gratings

Poster and oral presentations by the undergraduate students

Here are some PHOTOS of the presentations.

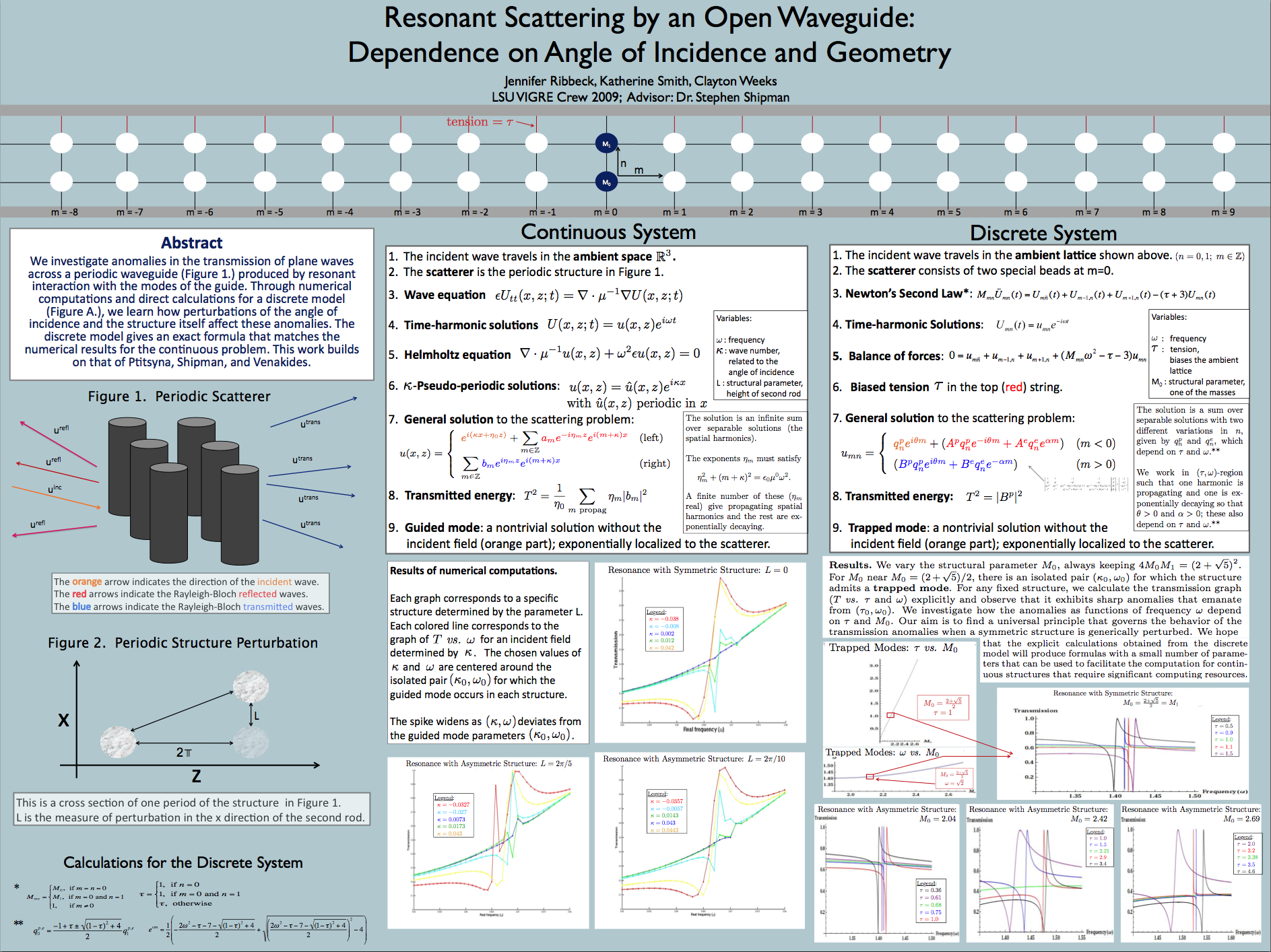
TEAM R: Jennifer Ribbeck, Kathy Smith, Clayton Weeks

Resonant Scattering by an Open Waveguide: Dependence on Angle of Incidence and Geometry

This project was presented at the annual meeting of SIAM in Denver in July, 2009.

A paper based on the results has been published in the IEEE Photonics Journal, Vol. 2, No. 6 (2010) 911-923. A preprint is available here.

Abstract: The team performed numerical computations of resonant energy transmission of plane waves across periodic dielectric rod structures and compared the results to exact calculations on a discrete model. They used a boundary-integral numerical code, for which they wrote a graphical user interface. The object is to obtain an analytic understanding of the behavior of transmission anomalies, due to interaction with trapped modes of the structure, as the frequency, angle of incidence, and geometry is varied. The ideas are based on Ref. 4 below.

Poster

Presentation	GUI

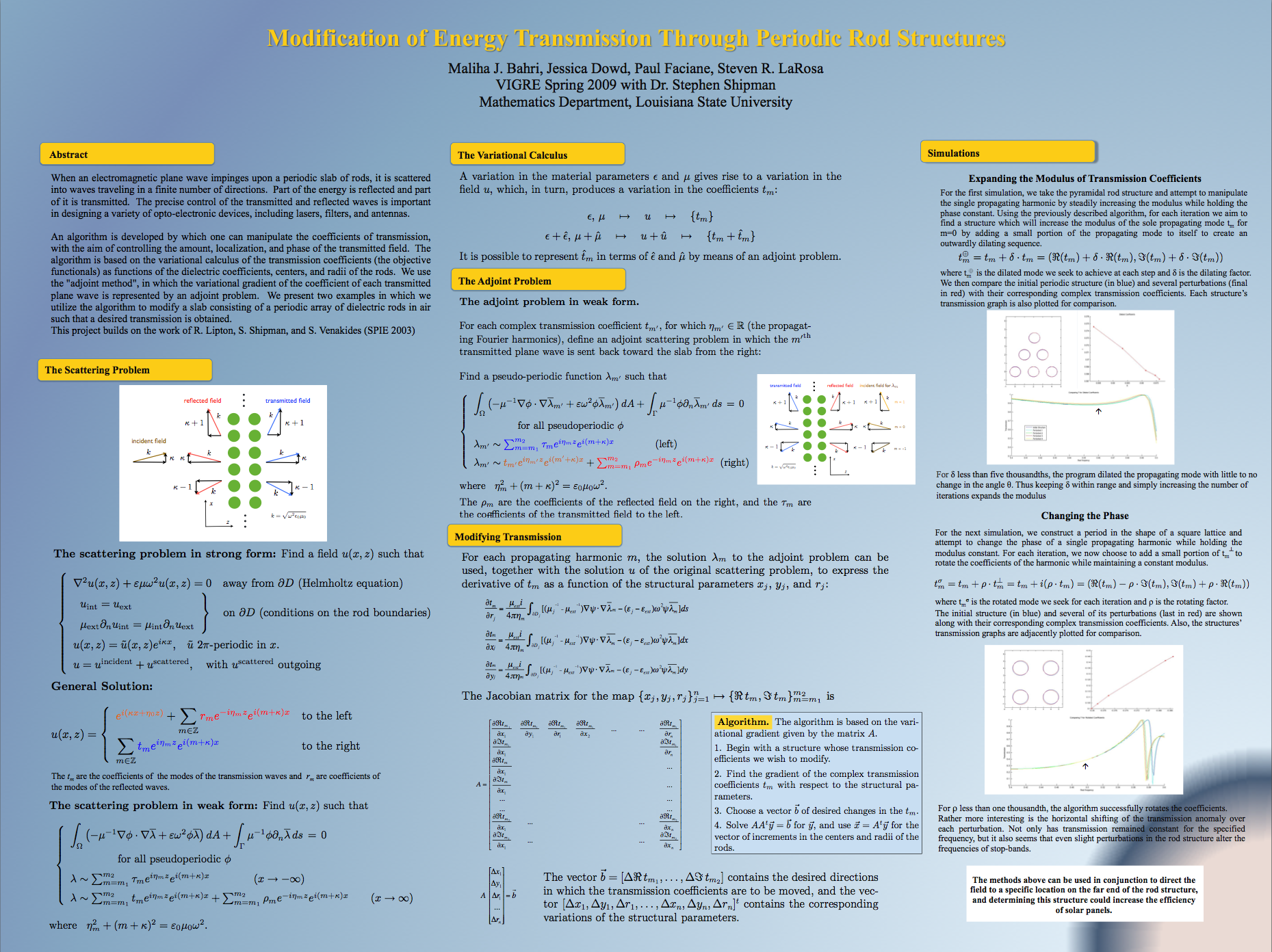
TEAM O: Maliha Bahri, Jessica Dowd, Paul Faciane, Steven LaRosa

Modification of Energy Transmission Through Periodic Rod Structures

Abstract: The team developed the variational calculus for the complex coefficients of the Rayleigh-Bloch waves transmitted across a periodic scatterer, under illumination by a plane wave, in terms of an adjoint scattering problem. They developed an algorithm that allows the real and imaginary parts of all transmitted waves to be modified individually. They adapted a boundary-integral numerical code to implement the algorithm and wrote a graphical user interface. The ideas are based on Ref. 3 below.

Poster

Presentation	GUI

Presentation:
Jennifer Ribbeck, Kathy Smith, and Clayton Weeks each presented a part of the oral exposition of Team R. Maliha Bahri, Paul Faciane, and Steven LaRosa each presented a part of the oral exposition of Team O. Jessica Dowd presented an overview to the common topic of both teams, which included some simulations that had been previously done using the boundary-integral numerical code that both teams used.

Overview

Syllabus and Schedule

Description. This is a "Vertically Integrated Research" course. Its structure is like that of a seminar, in which professors, post-docs, graduate students, and undergraduate students participate. The aims are

(1) to give the participants relatively broad exposure to electromagnetic, acoustic, and elastic waves in composite media and computational techniques;

(2) to delve in depth into the details of a specific problem;

(3) to develop effective presentation skills;

(4) to gain exposure to specialized areas of mathematics involved in the physical problems.

Credit. Both graduate and undergraduate students can enroll for this course. For undergraduates, it counts toward the three credits of capstone course that are required for the math major.

Prerequisites. Math 2057 (multivariable calculus) for undergraduate students; Math 7311 (real analysis) for graduate students.

Structure. The main components of the course are

Lectures:

Introductory lectures by Prof. Shipman on waves in periodic structures

Lectures by graduate students on special topics (S. Fortes, S. Jimenez, H. Ngo, H. Tu)

Lectures by other faculty

Participation in the Applied Analysis Seminar

Projects:

Projects of the undergraduate participants

Oral and poster presentations of the projects

Mentoring:

Graduate students and professors will happily mentor undergraduate students.

Projects. The projects will involve theory, literature research, and/or scientific computation and computer programming, and may be group efforts. The results will be presented

(1) in a written paper,

(2) on a professional-style poster, and

(3) orally in a forum open to the public.

Evaluation. There will be no exams or regular assignments, but students may be asked to present their work orally or in written fashion occasionally throughout the semester. Evaluation of performance in the course is based on participation and the quality of the project, in written, poster, and oral presentation.

1. Resonant scattering by periodic waveguides.
Members: Ben Chutz, Jennifer Ribbeck, Kathy Smith, Clayton Weeks

This project investigates the anomalous scattering behavior that occurs when acoustic or electromagnetic plane waves emanating from sources exterior to a subwavelength periodic waveguide interact with the guided modes of the structure. A case of anomalous transmission of energy similar to that studied in Ref. 4 below is analyzed numerically using a boundary-integral code developed in Ref. 2, with an additional structural asymmetry parameter. A rigorous discrete model that illustrates the essential characteristics of the continuous problem is explicitly worked out, giving an exact formula for a transmission anomaly that is expected qualitatively to match that of the continuous problem and thus provide a method of predicting the forms of the anomalies. The team will also develop a graphical user interface (GUI) that allows a user to enter parameters of a periodic waveguide consisting of arrays of rods and compute the graph of the transmission coefficient with the click of a button.

2. Optimization of scattering by periodic slabs.
Members: Maliha Bahri, Jessica Dowd, Paul Faciane, Steven LaRosa

This project aims to develop an algorithm by which one can manipulate certain features of the acoustic or electromagnetic field resulting from the scattering of a plane wave by a periodic structure. The techniques build on those developed in Ref. 3 below, in which a gradient-flow algorthm for manipulating the transmitted power across a periodic slab was developed by constructing the adjoint scattering problem that characterizes the variational gradient of the transmission functional. In this project, the variational calculus will be extended to other objective functionals, namely, the complex coefficients of the scattered Rayleigh-Bloch waves. The aim is to design subwavelength structures that can channel incident radiation into specific spots at the back side of the slab at which frequency-specific absorbers can be placed for photoelectric conversion. The team will also develop a GUI that will implement the gradient algorithm using a boundary-integral numerical code developed in Ref. 2.

Schedule:

Jan. 13	Introduction to the course
Jan. 15	A look at phenomena and numerical simulations in scattering by periodic slabs. See the link Research/Topics in the navigation bar on this page.
Jan. 20	Begin discussion of the mathematics: the wave equation
Jan. 22	Seminar on Financial Mathematics
Jan. 27	The wave equation and the Helmholtz equation: oscillations and traveling waves
Jan. 29	Continuation of the Helmholtz equation
Feb. 3	Introduction of the computational code and file-sharing system
Feb. 5	Alvaro Guevara: How to build a GUI, in the computer lab Lockett 233
Feb. 10	Alvaro Guevara: Continuation of GUI building, Lockett 233
Feb. 12	Undergraduate student presentations. See notes below posted Feb. 5.
Feb. 17	Diffraction by a periodic structure: analysis by space harmonics
Feb. 19	The Mathematics of Resonance and Optimization. See notes below posted Feb. 12.
Feb. 26	More on Resonance and Optimization. Continuation of discussions.
Mar. 3, 10	Hairui Tu: Integral equations for the Helmholtz equation
Mar. 5	Separate discussions with the two groups.
Mar. 12, 17	Silvia Jimenez: Homogenization theory
Mar. 19	Santiago Fortes: Waves in dielectric/plasmonic composites
Mar. 24	Santiago Fortes: COMSOL Multiphysics package, Lockett 233
Mar. 26	Work on projects.
Mar. 31	Prof. Robert Lipton: From Dido's problem to polarization tensors: A brief history of isoperimetric inequalities.
Apr. 2 +	Continue work on the team projects. Start writing your techincal reports.
Apr. 20 (Mon.)	Prof. David Dobson: Applied Analysis Seminar, Lockett 285
Apr. 23	Hai Ngo: Scattering by a corrugated surface
May 5	12:00-2:00: Poster and oral presentations in the Keisler Lounge

Notes:

»Posted Feb. 5.

1. You can start now to think out your GUI for executing the scattering code. Think of what information you want the user to enter, which pushbuttons you need, etc., and build the skeleton. The code will be added as we learn more about GUIs.

2. Keep working on reproducing the graphs in the papers I gave you. You will see "Undergraduate student presentations" on the class schedule for Thurs., Feb. 12. That means that each group will present graphs of its transmission calculations to everyone else, using the overhead projector. Besides the graphs in the papers, do some numerical experiments of your own by creating new input files. You may also present your GUI skeletons.

Go ahead and create a subdirectory called matlab (mkdir matlab) in your "optimization" or "resonance" directory that will contain all your matlab stuff, and have someone in your group commit it to the repository. Decide on how you want to organize your files, so everyone is in agreement. Decide how the tasks will be assigned within your group--not everyone needs to work on the same task, but each member should keep up with and approve of what the others do.

BTW, the file called "xyfile" in the repository contains points on the circles of the structure you last executed with "scatter". If you graph those points with some graphics application, you will see the structure.

»Posted Feb. 12.

On Tuesday, Feb. 17, we will discuss the mathematics of scattering of plane waves by a periodic structure. This will involve Fourier series, plane wave solutions of the Helmholtz equation, and Rayleigh-Bloch waves. This will be important for understanding the mathematics of your problems. I will write notes for this before class and update the pdf file below. As preparation, googling these topics will be helpful.

On Thursday, Feb. 19, I want to discuss each of the groups' problems and goals. As I work with one group, the other group will work separately, and the graduate students will participate. As preparation for this session, I want each group to have devised some kind of numerical experiment and done simulations. The purpose of this is to get you thinking actively about the physics. Your experiment can be anything that you think is interesing. Of course, you may (and are encouraged to) talk to me or the graduate students about your thoughts.

In the meantime, get your GUI to the point where it takes user input, runs the scattering code, and returns the results (as a graph, for example).

Documents:
Syllabus
Notes on the mathematics
Guide for designing posters (ppt)
Matlab tutorial
How to use file sharing

Literature:

[1] Photonic Crystals: Molding the Flow of Light, J. D. Joannopoulos, R. D. Meade, J. N. Winn, Princeton University Press, 1995.

[2] Boundary-Integral Calculations of Two-Dimensional Electromagnetic Scattering in Infinite Photonic Crystal Slabs: Channel Defects and Resonances, M. Haider, S. Shipman, and S. Venakides, SIAM J. Appl. Math., Vol. 62 (2002), No. 6, pp. 2129-2148.

[3] Optimization of Resonances in Photonic Crystal Slabs, R. Lipton, S. Shipman, and S. Venakides, Proceedings of SPIE, Vol. 5184 (2003), pp. 168-177.

[4] Resonant transmission near non-robust periodic slab modes, S. Shipman and S. Venakides, Physical Review E, Vol. 71, 1 (2005), 026611-1-10.