Abstracts of talks at OAL2017
Conference on Order and Algebra in Logic (OAL2017)
Richard N. Ball (rball@du.edu; University of Denver) and Anthony W. Hager (ahager@wesleyan.edu; Wesleyan University). Pointfree pointwise convergence, Baire functions, and epimorphisms in truncated archimedean $\ell$-groups.
We define pointfree pointwise convergence, and use it to define the Baire functions on a locale. The main result is that the Baire functions on a locale coincide with the continuous functions on its $P$-locale coreflection. Furthermore, we show that the Baire functions on a locale constitute the epicompletion of the continuous functions in the relevant category.
The relevant category is $\mathbf{T}$, the category of truncated archimedean $\ell$-groups, hereafter nicknamed truncs. $\mathbf{T}$ is closely related to the famous category $\mathbf{W}$ of unital archimedean $\ell$-groups. The universal objects in $\mathbf{T}$ are of the form $\mathcal{R}_0 L$, the trunc of real-valued locale maps $L \to \mathbb{R}$ which vanish at the designated point of $L$.
We provide an intuitive definition of pointwise convergence in $\mathcal{R}_0 L$ which extends the classical definition, and show that it has a number of nice properties: all homomorphisms and operations are pointwise continuous, and a pointwise dense extension is a trunc epimorphism. Conversely, we show that every epic extension $G \to H$ has an epic extension $H \to K$ such that $G$ is pointwise dense in $K$.
We show that the rich theory of epimorphisms in $\mathbf{W}$ carries over to $\mathbf{T}$ with only minor modification. In particular, the epicomplete truncs comprise a full monoreflective subcategory, and are characterized as those objects of the form $\mathcal{R}_0 P$ for a $P$-locale $P$. In light of these facts, a reformulation of the last clause of the preceding paragraph is that any trunc is pointwise dense in any epicompletion. And a trunc is epicomplete iff it is pointwise complete, i.e., has no proper extension in which it is pointwise dense.
Finally, for a given pointed locale $L$, we define the functions of Baire class $\alpha$ on $L$ in the classical fashion. A function is Baire class $0$ if it lies in $\mathcal{R}_0 L$, of Baire class $\alpha + 1$ if it is the pointwise limit of a sequence of functions of Baire class $\alpha$, and of Baire class $\beta$ for a limit ordinal $\beta$ if it is the pointwise limit of a sequence of functions of Baire class $\alpha < \beta$. A Baire function on $L$ is a function of Baire class $\alpha$ for some $\alpha$. Our results can be summarized as follows.$\vphantom{\chi_{\chi_{\chi_{\chi_{\chi_{\chi_\chi}}}}}}$
Theorem. For a pointed locale $L$ with $P$-locale coreflection $\mathcal{P}_* L \to L$, the Baire functions on $L$ are precisely the continuous functions on $\mathcal{P}_* L$, i.e., those of $\mathcal{R}_0 \mathcal{P}_* L$.$\vphantom{\chi_{\chi_{\chi_{\chi_{\chi_{\chi_\chi}}}}}}$
Theorem. The embedding $\mathcal{R}_0 L \to \mathcal{R}_0 \mathcal{P}_* L$ is the functorial epicompletion in $\mathbf{T}$.
Papiya Bhattacharjee (bpapiya@gmail.com; Pennsylvania State University at Erie) and Warren McGovern (Wmcgove1@fau.edu; Florida Atlantic University). Lamron $\ell$-groups.
An $\ell$-group $G$ is called lamron if $\mathop{\rm Min}(G)^{-1}$ is a Hausdorff topological space, where $\mathop{\rm Min}(G)^{-1}$ is the space of all minimal prime subgroups of $G$ endowed with the inverse topology. The speaker will discuss various features of lamron $\ell$-groups and their relation to $\ell$-groups with stranded primes, and complemented $\ell$-groups.
Gerard Buskes (University of Mississippi, Oxford, MS) and R. H. Redfield (rredfiel@hamilton.edu; Hamilton College, Clinton, NY). Extending Cauchy-continuous maps on lattice-ordered groups.
We investigate Cauchy-continuous maps from Archimedean lattice-ordered groups to themselves. We are especially interested in extending Cauchy-continuous group-automorphisms to Dedekind completions and determining what properties are preserved by such extensions.
Frederick K. Dashiell, Jr. (dashiell@math.ucla.edu; Chapman University/University of California at Los Angeles). Distributive joins, relative annihilators, and the lattice of cozero sets.
We begin with a journey through some familiar scenery in partially ordered sets, and some old but not-so-familiar scenery as well. We seek extensions of a poset to a lattice which has nice completeness and distributivity properties, such as a frame has. We then apply this process to the lattice $L$ of cozero sets in a topological space. Using the relation rather below in a bounded distributive lattice, which models the topological relation $\overline{A}\subset B$, and the notion of a regular lattice, which models a regular topological space, we arrive at a direct proof of Moshier's result that the normal completion (which we learned about long ago) of such $L$, is actually a frame. In fact, the MacNeille completion of any regular lattice is a frame. The description employs relative annihilators, i.e., ideals of the form $\{x: x\wedge a\le b\}$. These are used establish a criterion for quasi-F frames which depends only on the cozero part.
Themba Dube (dubeta@unisa.ac.za), University of South Africa. A result of Larson made algebraic.
An $f$-ring is called quasi-normal if the sum of any two different minimal prime $\ell$-ideals is either a maximal $\ell$-ideal or the entire ring. Recall that for a Tychonoff space $X$ and $p\in\beta X$, the ideal $O^p$ of $C(X)$ consists of those $f$ for which $\mathop{\rm cl}_{\beta X}Z(f)$ is a neighbourhood of $p$, where $Z(f)$ is the zero-set of $f$. In 1995 Susan Larson proved that the ring $C(\beta X)$ is quasi-normal if and only if $C(X)$ is quasi-normal and the ideal $O^p$ is prime whenever the maximal ideal $M^p$ is hyper-real. In this talk I will show that this result is actually a corollary of a purely ring-theoretic theorem about $f$-rings that are more general than rings of continuous functions.
José F. Fernando (josefer@mat.ucm.es), Departamento de Álgebra, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040 MADRID (SPAIN). A substitution theorem for rings of semialgebraic functions and applications.
Let $R\subset F$ be an extension of real closed fields and ${\mathcal S}(M,R)$ the ring of (continuous) semialgebraic functions on a semialgebraic set $M\subset R^m$. We show that every $R$ homomorphism $\varphi:{\mathcal S}(M,R)\to F$ is essentially the evaluation homomorphism at a certain point $p\in F^m$ adjacent to the extended semialgebraic set $M_F$. This type of result is commonly known in Real Algebra as Substitution Theorem. In case $M$ is locally closed, the results are neat, whereas the non locally closed case requires a more subtle approach and some auxiliary results of geometric nature (weak continuous extension theorem, appropriate immersion of semialgebraic sets) that have interest on their own. We also afford the same problem for the ring ${\mathcal S}^*(M,R)$ of bounded (continuous) semialgebraic functions getting results of a rather different nature. Substitution theorems can be used for instance to understand the properties of some prime and maximal ideals of the rings ${\mathcal S}(M,R)$ and ${\mathcal S}^*(M,R)$.
Goulwen Fichou (goulwen.fichou@univ-rennes1.fr), Université de Rennes; visiting UBC at Vancouver. Sum of squares of continuous rational functions.
Rational functions on an affine space admitting a continuous extension at their poles have been recently studied as a tame class of functions between regular and semi-algebraic functions. In the talk, we will discuss some properties of the ring of continuous rational functions from the point of view of real algebra.
Wesley Fussner (wesley.fussner@du.edu), University of Denver. Representing involutive residuated lattices.
We take initial steps toward developing a representation theory for involutive residuated lattices by giving a novel representation theorem for Sugihara monoids. These algebras are idempotent, commutative, involutive residuated lattices, and have been proposed as models of reasoning in the presence of contradictory information. The main result of this work is that each Sugihara monoid is isomorphic to an algebra of continuous homomorphisms between appropriately-defined topological structures. Being grounded in the Davey-Werner duality for lattices with involution, this representation theorem places the involutive residuated lattice character of the Sugihara monoids at the forefront.
Andrew Glass (A.M.W.Glass@dpmms.cam.ac.uk), Queens' College, Cambridge CB3 9ET, England. Recognizing the real line (joint work with John S. Wilson).
Let $(\Omega, \leq)$ be a totally ordered set. We prove that if $\mathop {\rm Aut}(\Omega,\leq)$ is transitive and satisfies the same first-order sentences as $\mathop {\rm Aut}(\mathbb R,\leq)$ (in the language of groups), then $\Omega$ and $\mathbb R$ are isomorphic ordered sets. This improvement of a theorem of Gurevich and Holland is obtained as one of many consequences of a study of centralizers associated with certain transitive subgroups of $\mathop {\rm Aut}(\Omega,\leq)$.
A.W. Hager (ahager@wesleyan.edu), Wesleyan University. Compact Condensations and Compactifications (joint work with W.W. Comfort and J. van Mill).
A Tychonoff space will be called Bicompactly Condensable (BC) if its topology contains a compact Hausdorff topology (i.e., there is a continuous bijection of $X$ onto a compact Hausdorf space). In the 1930's P.S. Alexandroff asked "What spaces are BC?", and in 1948, S. Banach asked that for metrizable spaces. Various authors have responded with special results, but it seems there is no succinct answer. Some are (the irrationals), and some are not (the rationals).
We call $X$ Strongly BC if its topology is the supremum of some set $S$ of compact Hausdorff topologies. Such $S$ determines a compactification of $X$ (embed in the product), and different $S$ can give different compactifications. We examine which compactifications of an SBC $X$ arise in this way: For some $X$, all do, and for others, some don't. For some $X$, the Cech-Stone compactification does, and for others, does not.
Oghenetega Ighedo (Ighedo@unisa.ac.za), University of South Africa. On the $z$-ideal functor.
An ideal $I$ of a commutative ring $A$ with identity is called a $z$-ideal if whenever two elements of $A$ belong to the same maximal ideals and one of the elements is in $I$, then so is the other. For a completely regular frame $L$ we denote by $\mathop{\rm Zid}(\mathcal{R}L)$ the lattice of $z$-ideals of the ring $\mathcal{R}L$ of continuous real-valued functions on $L$. It is a coherent frame, and it is known that $L\mapsto\mathop{\rm Zid}(\mathcal{R}L)$ is the object part of a functor $\mathsf{Z}\colon\mathbf{CRFrm}\to\mathbf{CohFrm}$, where $\mathbf{CRFrm}$ is the category of completely regular frames and frame homomorphisms, and $\mathbf{CohFrm}$ is the category of coherent frames and coherent maps. In this talk I will explore when this functor preserves and reflects the property of being a Heyting homomorphism, and also when it preserves and reflects the variants of openness of Banaschewski and Pultr [1].
Reference:
[1] B. Banaschewski, A. Pultr: Variants of openness, Appl. Categor. Struct. 2 (1994), 331-350.
Purbita Jana (purbita.jana@gmail.com), University of Calcutta. Graded Frame vs Generalised Geometric Logic.
We introduce the concept of a generalized geometric logic (fuzzy geometric logic with graded consequence) which led us to propose the concept of graded frame. As a starting point we introduce the concept of generalised topological system which represents the interplay between generalized topological space and generalized geometric logic. This generalizes Vickers' concept of a topological system, which is a triple $(X,\models,A)$, consisting of a non-empty set $X$, a frame $A$, and a relation `$\models$', called a "satisfaction relation". Vickers relates the concept of topological system with so-called geometric logic, or logic of finite observations. Similarly, using suitable substructures of generalized topological space and generalized geometric logic, categorical equivalences and dualities are presented.
Jingjing Ma (Ma@uhcl.edu), University of Houston-Clear Lake. Directed Partial Orders on $C_F$ and $H_F$.
Let $F$ be a totally ordered field. Define $$C_F = F + Fi = \{\,a + bi\mid a, b\in F\,\}$$ and $$H_F = F + Fi + Fj + Fk = \{\,a + bi + cj + dk\mid a, b, c, d\in F\,\},$$ where $i^2 = j^2 = k^2 = -1$. $C_F$ and $H_F$ are called the field of complex numbers over $F$ and the division algebra of quaternions over $F$, respectively.
Let $\mathbb R$ be the totally ordered field of real numbers with the usual total order. It was proved that $C_{\mathbb R}$ cannot be a lattice-ordered algebra over $\mathbb R$ (Birkhoff & Pierce, 1956) and $H_{\mathbb R}$ cannot be a lattice-ordered algebra over $\mathbb R$ (McHaffey, 1962). In fact, $C_F$ and $H_F$ cannot be a lattice-ordered algebra over $F$ for any totally ordered field $F$.
In 2011, Schwartz and Yang showed that $C_{\mathbb R}$ can be made into a partially ordered field over $\mathbb R$ with a directed partial order if $\mathbb R$ is a non-archimedean totally ordered field.
If $F$ is an archimedean totally ordered field, then $C_F$ and $H_F$ cannot be made into a directed algebra over $F$. For a non-archimedean totally ordered field $F$, $C_F$ and $H_F$ can be made into directed algebra over $F$. Furthermore, all directed partial orders on $C_F$ over $F$ could be described.
James Madden (JamesJMadden@gmail.com), Louisiana State University. Rings of fractions of $f$-rings.
(No abstract.)
Jim McEnerney (mcenerney.math@gmail.com). A real Nullstellensatz with multiplicity.
Let $A$ be a commutative ring containing the rationals. Let $S$ be a multiplicatively closed subset such that $1\in S$ and $0\notin S$, $T$ a cone in $A$ such that $S\subset T$ and $I$ an ideal in $A$. Then $$\rho_{S,T}I=\{\,a\mid sa^{2m}+t\in I^{2m}\hbox{ for some }m\in\mathbb N,\hbox{ }s\in S\hbox{ and }t\in T\,\}$$ is an ideal. For a commutative ring the collection of non-reduced orders (total cones) is a fibration of the real spectrum. Both concepts carry information regarding multiple solutions in the constructible set associated with $I$, $T$ and $S$. When the ring is a real regular domain, a non-reduced Nullstellensatz is presented that extends the real Nullstellensatz and relates these concepts. The notion of real multiplicity is proposed and examined for elements that are either positive definite (PD) or positive semi-definite (PSD) on the real spectrum.
Warren McGovern (Wmcgove1@fau.edu; Florida Atlantic University) and Papiya Bhattacharjee (bpapiya@gmail.com; Pennsylvania State University at Erie). Spaces of Ultrafilters and Maximal $d$-subgroups.
W is the category of archimedean $\ell$-groups with distinguished weak order unit. For $(G,u)\in {\bf W}$, $YG$ denotes the Yosida space of $u$, a compact Hausdorff space, on which the Yosida Embedding Theorem represents $G$ as an $\ell$-group of continuous almost real-valued functions:
$$G\mapsto \hat{G}\subseteq D(YG)$$
with $\hat{G}$ separating points from closed subsets of $YG$.
The set of $G$-cozero-sets of $YG$ is denoted by $\mathop{\rm coz}(G)$ and it is known that
$$\mathop{\rm coz}(G)\subseteq\mathop{\rm coz}(YG),$$
the latter being the collection of cozero-sets of $YG$. We let $Z(G)$ denote the collection of $G$-zero-sets of $YG$ and it is known that $YG$ is homeomorphic to the space of $Z(G)$-ultrafilters.
The collection
$$Z^\#(G)=\{\mathop{\rm cl}\nolimits_{YG}\mathop{\rm int}\nolimits_{YG}Z(g):g\in G\}$$
is a sub-lattice of the boolean algebra of all regular closed subsets of $YG$. The space of $Z^\#(G)$-ultrafilters is homeomorphic to the space of maximal $d$-subgroups of $G$, $\mathop{\rm Max}_d(G)$. This results in a collection of
$\vphantom{\chi_{\chi_{\chi_{\chi_{\chi_{\chi_\chi}}}}}}$maps
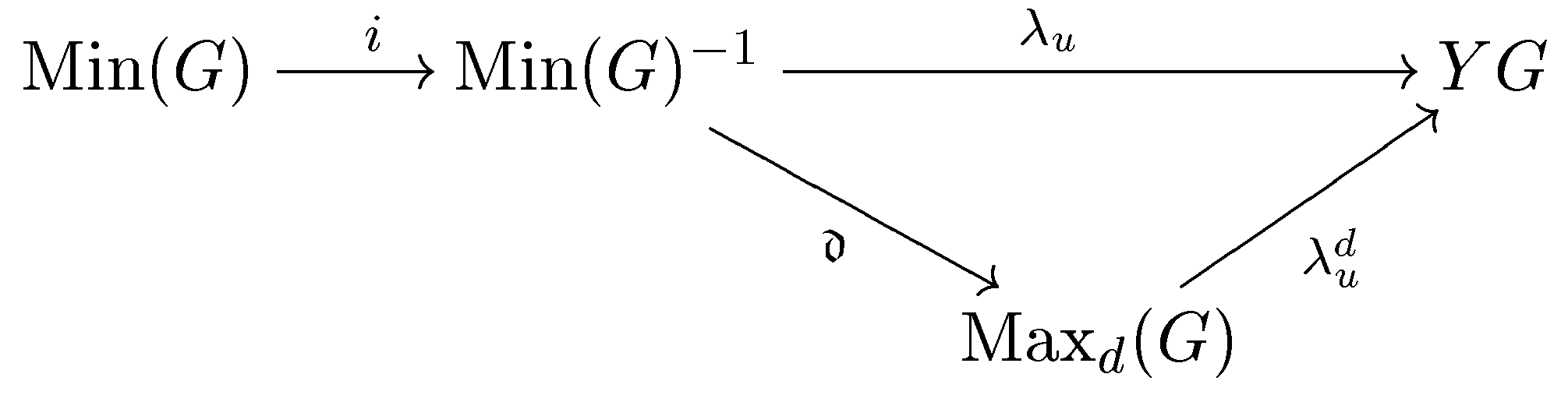 We$\vphantom{A^{A^{\hat{A}^{\hat{A}}}}}$ shall discuss the coincidence of these as well as when the maps are bijections.
We$\vphantom{A^{A^{\hat{A}^{\hat{A}}}}}$ shall discuss the coincidence of these as well as when the maps are bijections.
Imanol Mozo Carollo (imanol.mozo@ehu.eus; CECAT - Chapman University, and The University of the Basque Country). Discontinuous real functions on frames from a lattice-theoretic approach.
Arbitrary real functions on a frame $L$ were introduced by Gutiérrez Garcí a, Kubiak and Picado in [1]. The idea behind this approach is to replace $L$ by a discretization of it, the frame $\mathsf{S}(L)$ of sublocales of $L$. This otherwise very successful approach fails, however, to represent all classical functions, not even all semicontinuous functions, other than by analogy. Recently, this was mended by Picado and Pultr in [2] where they replace $\mathsf{S}(L)$ by a smaller class of sublocales, still following the idea of discretizing $L$.
The aim of the this talk is to present an alternative definition that arises from a lattice-theoretic approach. The lattice $\overline{\mathrm{F}}(X)$ of arbitrary extended real functions on a $T_1$-space $X$ is isomorphic to the Dedekind-MacNeille completion of the poset of all semicontinuous extended real functions defined on that space. Mimicking this situation, we will model discontinuous extended real functions in the pointfree setting in such a way that, if $L$ is a subfit frame, arbitrary real functions on $L$ are the elements of the Dedekind-MacNeille completion of the poset of all semicontinuous extended real functions on $L$.
References:
[1] J. Gutiérrez García, T. Kubiak, J. Picado,
Localic real functions: A general setting, J. Pure Appl. Algebra
213, (2009) 1064-1074.
[2] J. Picado and A. Pultr,
A Boolean extension of a frame and a representation of discontinuity,
Preprint 16-46 of DMUC, November (2016).
Ramiro H. Lafuente Rodriguez (Ramiro.LafuenteRodri@usd.edu), University of South Dakota. $n$-th Roots in the Group of Automorphisms of an o-Group of Finite Archimedean Rank.
We describe totally ordered groups of finite archimedean rank and their groups of ordered automorphisms. We provide criteria for the solvability of equations of the form $x^n=g$ in the group of ordered automorphisms of certain archimedean-complete totally ordered groups of finite archimedean rank.
Philip Scowcroft (pscowcroft@wesleyan.edu), Wesleyan University. Some lex-sums and lex-products with infinite basis.
After reviewing the lex-sums [lex-products] studied by Conrad [Jakubík-Dreveňák], I will show how Nullstellensätze for lex-products with finite basis remain true and may even be extended when the basis is infinite. If time permits I will mention results, true when the basis is finite, which either fail or remain unresolved when the basis is infinite.
Friedrich Wehrung (friedrich.wehrung01@unicaen.fr), Université de Caen, Campus 2 (France). Spectral spaces of Abelian lattice-ordered groups..
A topological space is spectral if it is sober and the compact open subsets form a basis of the topology, closed under nonempty finite intersection. It is well known that the spectrum of any Abelian lattice-ordered group with unit (equivalently, MV-algebra) is spectral and completely normal, the latter meaning that for any points $x$ and $y$ in the closure of a singleton $\{z\}$, either $x$ is in the closure of $\{y\}$ or $y$ is in the closure of $\{x\}$. A 1994 example by Delzell and Madden shows that the converse does not hold: not every completely normal spectral space is the spectrum of an Abelian lattice-ordered group with unit. However, this example is not second countable.
This talk aims at giving an idea of the proof that every second countable completely normal spectral space is the spectrum of an Abelian lattice-ordered group with unit. This proof starts by formulating the problem in terms of lattices of principal $\ell$-ideals of lattice-ordered groups. In the countable case, the lattices thus obtained are characterized by a first-order sentence, equivalent to the complete normality of the Stone dual. On the other hand, in the uncountable case, there is no $\mathcal{L}_{\infty,\omega}$ characterization (thus no first order characterization) of those lattices.
Brian Wynne (Brian.Wynne@Lehman.cuny.edu), Lehman College, CUNY. More on upper extensions of existentially closed Abelian lattice-ordered groups..
An Abelian $\ell$-group $G$ is existentially closed (e.c.) just in case every finite system of $\ell$-group equations and in-equations, involving elements of $G$, that is solvable in some Abelian $\ell$-group extending $G$ is solvable already in $G$. In previous OAL lectures, I described how one may use the upper extension construction of Ball, Conrad, and Darnel to produce examples of non-Archimedean e.c. Abelian $\ell$-groups. In this talk, I will present some refinements of my earlier results and some new examples.
| Attachment | Size |
|---|---|
| 20.36 KB |